题目内容
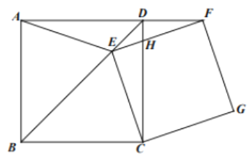
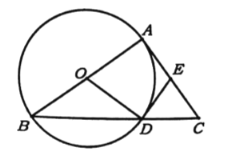
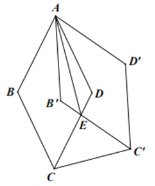
【题目】如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为![]() +2.其中正确结论的个数是
+2.其中正确结论的个数是
A.1B.2C.3D.4
【答案】B
【解析】
连结对角线![]() ,
,![]() ,∴
,∴![]() ,根据菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,得到
,根据菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,得到![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
∴![]() ,
,![]() ,并根据已知和菱形的性质可得:
,并根据已知和菱形的性质可得:![]() ∴
∴![]() ,
,![]() ,∴②不正确;
,∴②不正确;
可根据条件证明![]() ≌
≌![]() ,得到
,得到![]() ,并由
,并由![]() ,
,![]() 得到
得到![]() ≌
≌![]() ,∴①正确;∴
,∴①正确;∴![]() 为
为![]() 的角平分线,
的角平分线,
∴![]() (三线合一)∴③正确;根据
(三线合一)∴③正确;根据![]() ,求出
,求出![]() ,利用
,利用![]()
![]() ,∴
,∴![]()
∴![]() ,
, ![]()
∴四边形AB′ED的周长为:![]()
![]() ∴④不正确
∴④不正确
解:连结对角线![]() ,
,![]() ,∴
,∴![]() ,
,
∵菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,
∴![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
∴![]()
∴![]()
由题目已知和菱形的性质可得:![]()
∴![]()
∴![]()
∴![]() ,②不正确;
,②不正确;
在![]() 和
和![]() 中
中
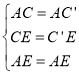
∴![]() ≌
≌![]()
∴![]()
∴由![]() ,
,![]()
∴![]() ≌
≌![]()
∴①正确;
∴![]() 为
为![]() 的角平分线,
的角平分线,
∴![]() (三线合一)
(三线合一)
∴③正确;
∵![]() ,
,
∴![]()
在菱形ABCD中,![]()
![]()
∴![]()
∴在![]() 中,
中,
![]() ,
, ![]()
∴四边形AB′ED的周长为:![]()
![]()
![]()
![]()
∴④不正确
综上所述,正确的有①③,
故选:B

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值