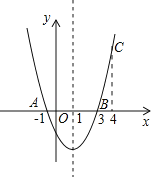题目内容
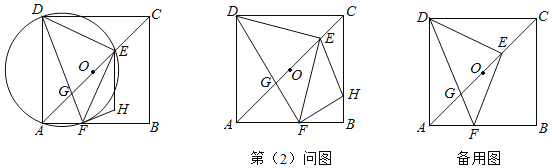
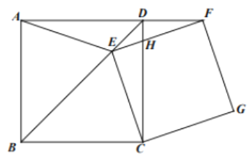
【题目】如图,在正方形ABCD中,E为对角线BD上的一点,点F在AD的延长线上,且∠CEF=90°,EF交CD于H,分别过点F,点C作EC和EF的平行线,交于点G.
(1)证明:AE=CE;
(2)证明:四边形ECGF是正方形;
(3)若正方形ABCD的边长为![]() ,且BE=BC,求此时ΔEDF的面积.
,且BE=BC,求此时ΔEDF的面积.
【答案】(1)见解析;(2)见解析;(3) ![]() .
.
【解析】
(1)利用AD=CD,∠ADE=∠CDE=45°,DE=DE,可得ΔADE≌ΔCDE(SAS),所以AE=CE;
(2)EF∥CG,EC∥FG,得四边形ECCF是平行四边形,并且∠CEF=90°,所以四边形ECGF是矩形,由三角形内角和可得∠DFH=∠ECH,并根据ΔADE≌ΔCDE,可以得到∠DFH=∠EAD,所以AE=EF,则由(1)可知CE=EF,所以四边形ECGF是正方形.
(3)作FM⊥BD,CN⊥BD,利用∠FEM+∠CEN=90°,∠FEM+∠EFM=90°,得到∠EFM=∠CEN,并根据∠M=∠CNE=90°,EF=EC,所以ΔFME≌ΔENC,FM=EN,EM=CN,
并RtΔBCD中,根据BE=BC=AB=![]() ,可得出EN=FM=BE-BN=
,可得出EN=FM=BE-BN=![]() -1,DE=BD-BE=2-
-1,DE=BD-BE=2-![]()
∴ΔEDF的面积![]() ,化简即可.
,化简即可.
证明:(1)在正方形ABCD中,
AD=CD,∠ADE=∠CDE=45°,
∵DE=DE
∴ΔADE≌ΔCDE(SAS)
∴AE=CE
(2)由题意,得EF∥CG,EC∥FG.

四边形ECCF是平行四边形
∵∠CEF=90°
∴四边形ECGF是矩形
∵∠HDF+∠DFH+∠DHF=∠CEH+∠ECH+∠EHC=180°
∠CEH=∠HDF=90°,∠DHF=∠EHC
∴∠DFH=∠ECH
由(1)得,ΔADE≌ΔCDE
∴∠EAD=∠ECD
∴∠DFH=∠EAD
∴AE=EF.
由(1)得,AE=CE
∴CE=EF
∵四边形ECGF是矩形
∴四边形ECGF是正方形.
(3)如图,作FM⊥BD,CN⊥BD,垂足分别为M、N

∵∠CEF=90°
∴∠FEM+∠CEN=90°,
∵∠FEM+∠EFM=90°,
∴∠EFM=∠CEN
∠M=∠CNE=90°,EF=EC
∴ΔFME≌ΔENC
∴FM=EN,EM=CN,
在RtΔBCD中,BE=BC=AB=![]() ,
,
∴BD=2,BN=DN=CN=1,
∴EN=FM=BE-BN=![]() -1,
-1,
∴DE=BD-BE=2-![]()
∴ΔEDF的面积![]()
![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
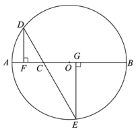
小学生10分钟应用题系列答案【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 上一动点,过点
上一动点,过点![]() 的直线交
的直线交![]() 于
于![]() 两点,且
两点,且![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,当点
,当点![]() 在
在![]() 上运动时,设
上运动时,设![]() ,
,![]() (当
(当![]() 的值为0或3时,
的值为0或3时,![]() 的值为2),探究函数
的值为2),探究函数![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
| 0 | 0. 40 | 0. 55 | 1. 00 | 1. 80 | 2. 29 | 2. 61 | 3 |
| 2 | 3. 68 | 3. 84 | 3. 65 | 3. 13 | 2. 70 | 2 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:点![]() 与点
与点![]() 重合时,
重合时,![]() 长度约为________
长度约为________![]() (结果保留一位小数).
(结果保留一位小数).