题目内容
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c的顶点坐标为P（2，9），与x轴交于点A，B，与y轴交于点C（0，5）．
（Ⅰ）求二次函数的解析式及点A，B的坐标；
（Ⅱ）设点Q在第一象限的抛物线上，若其关于原点的对称点Q′也在抛物线上，求点Q的坐标；
（Ⅲ）若点M在抛物线上，点N在抛物线的对称轴上，使得以A，C，M，N为顶点的四边形是平行四边形，且AC为其一边，求点M，N的坐标．
【答案】（1）y=﹣x2+4x+5，A（﹣1，0），B（5，0）；（2）Q（
，4）；（3）M（1，8），N（2，13）或M′（3，8），N′（2，3）．
【解析】
(1)设顶点式，再代入C点坐标即可求解解析式，再令y=0可求解A和B点坐标；
(2)设点Q（m，﹣m2+4m+5），则其关于原点的对称点Q′（﹣m，m2﹣4m﹣5），再将Q′坐标代入抛物线解析式即可求解m的值，同时注意题干条件“Q在第一象限的抛物线上”；
(3)利用平移AC的思路，作MK⊥对称轴x=2于K，使MK=OC，分M点在对称轴左边和右边两种情况分类讨论即可.
（Ⅰ）设二次函数的解析式为y=a（x﹣2）2+9，把C（0，5）代入得到a=﹣1，
∴y=﹣（x﹣2）2+9，即y=﹣x2+4x+5，
令y=0，得到：x2﹣4x﹣5=0，
解得x=﹣1或5，
∴A（﹣1，0），B（5，0）．
（Ⅱ）设点Q（m，﹣m2+4m+5），则Q′（﹣m，m2﹣4m﹣5）．
把点Q′坐标代入y=﹣x2+4x+5，
得到：m2﹣4m﹣5=﹣m2﹣4m+5，
∴m=或
（舍弃），
∴Q（，
）．
（Ⅲ）如图，作MK⊥对称轴x=2于K．
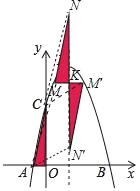
①当MK=OA，NK=OC=5时，四边形ACNM是平行四边形．
∵此时点M的横坐标为1，
∴y=8，
∴M（1，8），N（2，13），
②当M′K=OA=1，KN′=OC=5时，四边形ACM′N′是平行四边形，
此时M′的横坐标为3，可得M′（3，8），N′（2，3）．
