题目内容
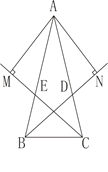
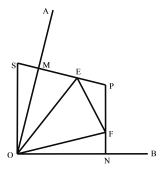
【题目】⑴如图1,点M、N分别在∠AOB的边OA、OB上,且OM=ON,过点M、N分别作MP⊥OA、NP⊥OB,MP、NP交于P,E、F分别为线段MP、NP上的点,且∠EOF=![]() ∠AOB,延长PM到S,使MS=NF,连接OS,则∠EOF与∠EOS的数量关系为 ,线段NF、EM、EF的数量关系为
∠AOB,延长PM到S,使MS=NF,连接OS,则∠EOF与∠EOS的数量关系为 ,线段NF、EM、EF的数量关系为
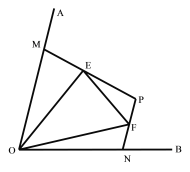
⑵如图2,点M、N分别在∠AOB的边OA、OB上,且OM=ON,![]() , E、F分别为线段MP、NP上的点,且∠EOF=
, E、F分别为线段MP、NP上的点,且∠EOF=![]() ∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
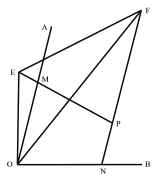
⑶如图3,点M、N分别在∠AOB的边OA、OB上,且OM=ON,![]() , E、F分别为线段PM、NP延长线上的点,且∠EOF=
, E、F分别为线段PM、NP延长线上的点,且∠EOF=![]() ∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
【答案】(1)相等,EF=FN+EM;(2)见解析;(3)见解析.
【解析】
(1)结论:相等,EF=FN+EM.先证明△OMS≌△ONF,再证明△OES≌△OEF即可解决问题.
(2)结论:EF=FN+EM.如图2中,延长EM到S,使得SM=FN,连接SO,先证明△OMS≌△ONF,再证明△OES≌△OEF即可解决问题.
(3)结论:EF=FN-EM.如图3中,延长ME到S,使得MS=FN,连接SO,先证明△OMS≌△ONF,再证明△OES≌△OEF即可解决问题.
理由:如图1中,
在△OMS和△ONF中,OM=ON,∠OMS=∠ONF,MS=FN,
∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=![]() ∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,OE=OE,∠SOE=∠EOF,OS=OF,
∴△OES≌△OEF,
∴EF=SE=SM+EM=FN+EM.
故答案为相等,EF=FN+EM.
(2)如图2中,延长EM到S,使得SM=FN,连接SO.

∵∠OMP+∠ONP=180°,∠OMS+∠OMP=180°,
∴∠OMS=∠ONF,
在△OMS和△ONF中,OM=ON,∠OMS=∠ONF,MS=FN,
∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=![]() ∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,OE=OE,∠SOE=∠EOF,OS=OF,
∴△OES≌△OEF,
∴EF=SE=SM+EM=FN+EM.
(3)结论:EF=FN-EM.
理由:如图3中,延长ME到S,使得MS=FN,连接SO.

∵∠OMP+∠ONP=180°,∠OMS+∠OMP=180°,
∴∠OMS=∠ONF,
在△OMS和△ONF中,OM=ON,∠OMS=∠ONF,MS=FN∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=![]() ∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,OE=OE,∠SOE=∠EOF,OS=OF,
∴△OES≌△OEF,
∴EF=SE=SM-EM=FN-EM.

 高中必刷题系列答案
高中必刷题系列答案