题目内容
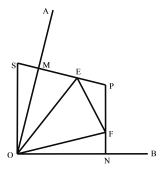
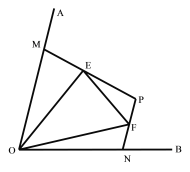
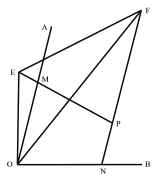
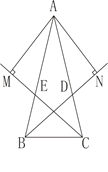
【题目】如图所示，在△ABC中，AB﹦AC，BD、CE分别是所在角的平分线，AN⊥BD于N点，AM⊥CE于M点。求证：AM﹦AN
【答案】见解析
【解析】
利用等边对等角证明∠ABC﹦∠ACB,根据角平分线证明∠ABD﹦∠ACE,由垂直证明Rt△AMC≌Rt△ANB(AAS),即可得到AM﹦AN.
证明：∵AB﹦AC（已知）
∴∠ABC﹦∠ACB（等边对等角）
∵BD、CE分别平分∠ABC、∠ACB（已知）
∴∠ABD﹦∠ACE
∵AM⊥CE, AN⊥BD（已知）
∴∠AMC﹦∠ANB﹦900(垂直的定义)
∴在Rt△AMC和Rt△ANB中
∠AMC﹦∠ANB, ∠ACM﹦∠ABN, AC﹦AB
∴Rt△AMC≌Rt△ANB(AAS)
∴AM﹦AN
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
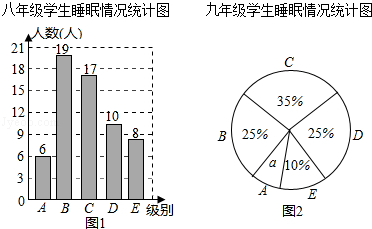
【题目】为了解某校八、九年级部分学生的睡眠情况，随机抽取了该校八、九年级部分学生进行调查，已知抽取的八年级与九年级的学生人数相同，利用抽样所得的数据绘制如图的统计图表：
睡眠情况分段情况如下
组别 | 睡眠时间x（小时） |
A | 4.5≤x＜5.5 |
B | 5.5≤x＜6.5 |
C | 6.5≤x＜7.5 |
D | 7.5≤x＜8.5 |
E | 8.5≤x＜9.5 |
根据图表提供的信息，回答下列问题：
（Ⅰ）直接写出统计图中a的值 
（Ⅱ）睡眠时间少于6.5小时为严重睡眠不足，则从该校八、九年级各随机抽一名学生，被抽到的这两位学生睡眠严重不足的可能性分别有多大？
