题目内容
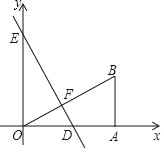
【题目】已知一次函数y＝kx+b的图象如图所示，
（1）求出这个函数关系式．
（2）图象上有一点P（4，m），求m的值．
（3）判断点（﹣4，3）和 （6，﹣6）是否在此直线上．
【答案】（1）y＝﹣1.5x+3；（2）m＝﹣3；（3）在，理由见解析.
【解析】
（1）由于点（0，3），（2，0）在函数y＝kx+b的图象上，则
，然后解方程组求出k、b即可得到一次函数解析式；
（2）把P（4，m）代入（1）中的解析式即可计算出m的值．
（3）分别把x＝﹣4，x＝6代入解析式判断即可．
解：（1）把（0，3），（2，0）代入y＝kx+b得
，解得
，
所以一次函数解析式为
（2）把P（4，m）代入
得m=﹣1.5×4+3=﹣3；
（3）把x=﹣4代入
，所以点（﹣4，3）不在直线上；
把x＝6代入y=﹣1.5×6+3=﹣6，所以点（6，﹣6）在直线上．
练习册系列答案
相关题目
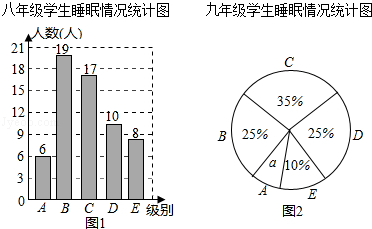
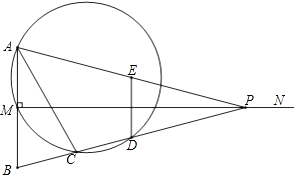
【题目】为了解某校八、九年级部分学生的睡眠情况，随机抽取了该校八、九年级部分学生进行调查，已知抽取的八年级与九年级的学生人数相同，利用抽样所得的数据绘制如图的统计图表：
睡眠情况分段情况如下
组别 | 睡眠时间x（小时） |
A | 4.5≤x＜5.5 |
B | 5.5≤x＜6.5 |
C | 6.5≤x＜7.5 |
D | 7.5≤x＜8.5 |
E | 8.5≤x＜9.5 |
根据图表提供的信息，回答下列问题：
（Ⅰ）直接写出统计图中a的值 
（Ⅱ）睡眠时间少于6.5小时为严重睡眠不足，则从该校八、九年级各随机抽一名学生，被抽到的这两位学生睡眠严重不足的可能性分别有多大？
