题目内容
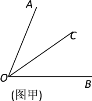
【题目】阅读下面材料:数学课上,老师给出了如下问题:如图甲,∠AOB=70°,OC平分∠AOB.
若∠BOD=20°,请你补全图形,并求∠COD的度数.
以下是小明的解答过程:
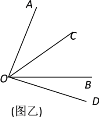
解:如图乙,因为OC平分∠AOB,∠AOB=70°,
所以∠BOC=____∠AOB=________°.
因为∠BOD=20°,
所以∠COD= °.
小静说:“我觉得这个题有两种情况,小明考虑的是OD在∠AOB外部的情况,事实上,OD还可能在∠AOB的内部” .
完成以下问题:
(1)请你将小明的解答过程补充完整;
(2)根据小静的想法,请你在图甲中画出另一种情况对应的图形,求出此时∠COD的度数.
【答案】(1)![]() ,35,55;(2)图见解析;
,35,55;(2)图见解析; ![]()
【解析】
(1)小明考虑的是OD边在∠AOB之外的情形,如此可知![]() ;
;
(2)根据小静的想法,可知还有可能OD边∠AOB之内,此时![]() .
.
(1)
解:如图乙,因为OC平分∠AOB,∠AOB=70°,
所以∠BOC=![]() ∠AOB=35°.
∠AOB=35°.
因为∠BOD=20°,
所以![]()
(2)作图如下:
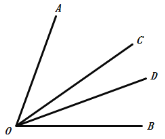
如图,因为OC平分∠AOB,∠AOB=70°,
所以∠BOC=![]() ∠AOB=35°.
∠AOB=35°.
因为∠BOD=20°,
所以∠COD=∠BOC-∠BOD=15°.

【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
A型 | B型 | |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
(3)若该商场预计用不少于2500元且不多于2600元的资金购进这批台灯,为了打开B种台灯的销路,商场决定每售出一盏B种台灯,返还顾客现金a元(10<a<20),问该商场该如何进货,才能获得最大的利润?
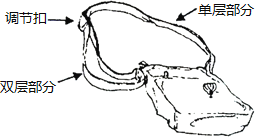
【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.乐乐用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)增长或缩短.经测量,得到如下数据:
单层部分的长度(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度(cm) | … | 73 | 72 | 71 |
| … | 0 |
(1)根据上表中数据的规律,填写表格中空白处的数据;
(2)设单层部分的长度为xcm,请用含x的代数式表示出双层部分的长度 cm;
(3)根据乐乐的身高和习惯,挎带的长度为110cm时,背起来最舒适,请求出此时单层部分的长度.