Question

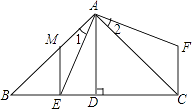
【题目】如图，四边形中， ，平分，点是延长线上一点，且．

（1）证明：；

（2）若与相交于点，，，求的长.

Answer 1

【答案】（1）证明见解析（2）

【解析】

试题分析：（1）直接利用等腰三角形的性质结合互余的定义得出∠BDC=∠PDC；

（2）首先过点C作CM⊥PD于点M，进而得出△CPM∽△APD，求出EC的长即可得出答案．

试题解析：（1）∵AB=AD，AC平分∠BAD，

∴AC⊥BD，

∴∠ACD+∠BDC=90°，

∵AC=AD，

∴∠ACD=∠ADC，

∴∠ADC+∠BDC=90°，

∴∠BDC=∠PDC；

（2）解：过点C作CM⊥PD于点M，

∵∠BDC=∠PDC，

∴CE=CM，

∵∠CMP=∠ADP=90°，∠P=∠P，

∴△CPM∽△APD，

∴ ，

设CM=CE=x，

∵CE：CP=2：3，

∴PC=x，

∵AB=AD=AC=1，

∴ ，

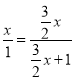解得：x=，

故AE=1﹣=．