Question

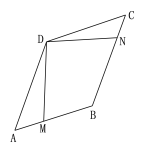
【题目】如图，边长为2的菱形ABCD中，∠A=60，点M是边AB上一点，点N是边BC上一点，且∠ADM=15，∠MDN=90，则点B到DN的距离为( )

A. B. C. D. 2

Answer 1

【答案】B

【解析】

连接BD，作BE⊥DN于E，利用菱形的性质和已知条件证得△ABD和△BCD是等边三角形，从而证得BD=AB=AD=2，∠ADB=∠CDB=60°，进而证得△BDE是等腰直角三角形，解直角三角形即可求得点B到DN的距离．

解：连接BD，作BE⊥DN于E，

∵边长为2的菱形ABCD中，∠A=60°，

∴△ABD和△BCD是等边三角形，

∴BD=AB=AD=2，∠ADB=∠CDB=60°

∵∠A=60°，

∴∠ADC=180°-60°=120°，

∵∠ADM=15°，∠MDN=90°，

∴∠CDN=120°-15°-90°=15°，

∴∠EDB=60°-15°=45°，

∴BE=BD=，

∴点B到DN的距离为，

故选：B．