题目内容
【题目】从A,B两题中任选一题解答,我选择________.
A.如图(1)是两棵树在同一盏路灯下的影子.
(1)确定该路灯泡所在的位置;
(2)如果此时小颖所在位置恰好与这两棵树所在的位置共线(三点在一条直线上),请画出图中表示小颖影子的线段AB.
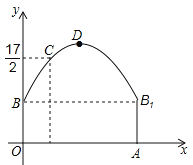
B.如图(2),小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他在某一灯光下的影子为DA,继续按此速度行走2秒到达点F,此时他在同一灯光下的影子落在其身后的线段DF上,测得此时影长MF为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H.他在同一灯光下的影子恰好是HB.图中线段CD,EF,GH表示小明的身高.

(1)请在图中画出小明的影子MF;
(2)若A、B两地相距12米,则小明原来的速度为______.
【答案】见解析;A.(1)见解析;(2)见解析;B.(1)见解析;(2)1.5 m/s.
【解析】
A.(1)利用中心投影的定义画图;(2)过点O作射线OB,交地面于点B,
B.(1)利用中心投影的定义画图;(2)设小明原来的速度为xm/s,则CE=2xm,AM=AF-MF=(4x-1.2)m,EG=2×1.5x=3xm,BM=AB-AM=12-(4x-1.2)=13.2-4x,根据相似三角形的判定方法得到△OCE∽△OAM,△OEG∽△OMB,则![]() =
=![]() ,
,![]() =
=![]() ,所以
,所以![]() =
=![]() ,即
,即![]() =
=![]() ,然后解方程即可.
,然后解方程即可.
解:从A,B两题中任选一题解答,我选择A,
A.(1)如图(1),
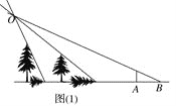
(2)如图所示,线段AB即为所求线段,
B.(1)如图(2),
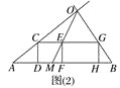
(2)设小明原来的速度为xm/s,则CE=2xm,AM=AF-MF=(4x-1.2) m,EG=2×1.5x=3xm,BM=AB-AM=12-(4x-1.2)=13.2-4x,
∵点C,E,G在一条直线上,CG∥AB,
∴△OCE∽△OAM,△OEG∽△OMB,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得x=1.5,
经检验x=1.5为方程的解,
∴小明原来的速度为1.5 m/s,
故答案为:1.5 m/s.

 阅读快车系列答案
阅读快车系列答案