题目内容

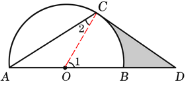
【题目】如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°.

（1）求证：CD是⊙O的切线；

（2）若⊙O的半径为2，求图中阴影部分的面积.

【答案】（1）证明见解析；（2）..

【解析】

试题（1）要证CD是⊙O的切线，只要证CD垂直于过切点的半径即可.

（2）要求图中阴影部分的面积，只要求出△OCD的面积和扇形OCB的面积即可.

试题解析：（1）如图，连接OC.

∵ AC＝CD，∠ACD＝1200，∴ ∠A＝∠D＝300.

∵ OA＝OC,∴ ∠2＝∠A＝300. ∴∠OCD＝∠ACD－∠2＝900.

∴ CD是⊙O的切线.

（2）∵∠A＝30o， ∴ ∠1＝2∠A＝600. ∴.

在Rt△OCD中, CD ＝OCtan600＝，

∴.

∴ 图中阴影部分的面积为.

练习册系列答案
相关题目

【题目】如图，ABCD的对角线AC、BD相交于点M，点M在以AB为直径的⊙O上，AD与⊙O相交于点E，连接ME．

(1)求证：ME＝MD；

(2)当∠DAB＝30°时，判断直线CD与⊙O的位置关系，并说明理由．

【题目】如图，直线AB和抛物线的交点是A(0，-3)，B(5，9)，已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标；

(2)在轴上是否存在一点C，与A，B组成等腰三角形？若存在，求出点C的坐标，若不存在，请说明理由；

(3)在直线AB的下方抛物线上找一点P，连接PA，PB使得△PAB的面积最大，并求出这个最大值.

【题目】已知抛物线y1＝﹣x2+mx+n，直线y2＝kx+b，y1的对称轴与y2交于点A（﹣1，5），点A与y1的顶点B的距离是4．

（1）求y1的解析式；

（2）若y2随着x的增大而增大，且y1与y2都经过x轴上的同一点，求y2的解析式．

【题目】已知抛物线y1＝x2+mx+n，直线y2＝2x+1，抛物线y1的对称轴与直线y2的交点为点A，且点A的纵坐标为5．

（1）求m的值；

（2）若点A与抛物线y1的顶点B的距离为4，求抛物线y1的解析式；

（3）若抛物线y1与直线y2只有一个公共点，求n的值．

【题目】如图，△ABC的顶点坐标分别为A(1，3)、B(4，2)、C(2，1)．

(1)作出与△ABC关于x轴对称的△A1B1C1，并写出A1、B1、C1的坐标；

(2)以原点O为位似中心，在原点的另一侧画出△A2B2C2，使．

【题目】从A，B两题中任选一题解答，我选择________．

A．如图(1)是两棵树在同一盏路灯下的影子．

(1)确定该路灯泡所在的位置；

(2)如果此时小颖所在位置恰好与这两棵树所在的位置共线(三点在一条直线上)，请画出图中表示小颖影子的线段AB.

B．如图(2)，小明从点A出发沿AB方向匀速前进，2秒后到达点D，此时他在某一灯光下的影子为DA，继续按此速度行走2秒到达点F，此时他在同一灯光下的影子落在其身后的线段DF上，测得此时影长MF为1.2米，然后他将速度提高到原来的1.5倍，再行走2秒到达点H.他在同一灯光下的影子恰好是HB.图中线段CD，EF，GH表示小明的身高．

(1)请在图中画出小明的影子MF；

(2)若A、B两地相距12米，则小明原来的速度为______．

【题目】如图，在平行四边形ABCD中，P是CD边上的一点，AP与BP分别平分∠DAB和∠CBA．

(1)判断△APB是什么三角形，证明你的结论；

(2)比较DP与PC的大小；

(3)画出以AB为直径的⊙O，交AD于点E，连接BE与AP交于点F，若tan∠BPC＝，求tan∠AFE的值．

【题目】如图，在圆O中，弦AB＝8，点C在圆O上(C与A，B不重合)，连接CA、CB，过点O分别作OD⊥AC，OE⊥BC，垂足分别是点D、E．

(1)求线段DE的长；

(2)点O到AB的距离为3，求圆O的半径．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网