题目内容
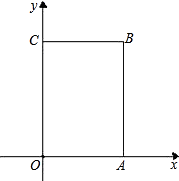
【题目】如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(2,0),其中a、b满足![]() , DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
, DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
(1)求A、B、E三点的坐标;
(2) 若以AB为一边在第二象限内构造等腰直角三角形△ABF,请直接写出点F的坐标.
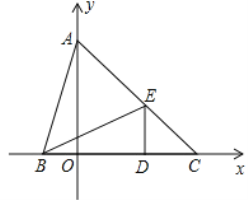
【答案】(1)A(0,3),B(-1,0),E(2,1),(2) (-4,1)(-3,4)(-2,2)
【解析】
(1)先根据非负数的性质求出a、b的值,进而可得出A、B两点的坐标;由已知角相等,加上一对直角相等,且根据A,B与D的坐标确定出OA=BD,利用AAS得到△AOB与△BED全等,利用全等三角形的对应边相等得到OB=ED,进而确定出E坐标.
(2)分∠BAF=90°,∠ABF=90°或∠AFB=90°三种情况进行讨论.
解:(1)∵a、b满足![]() +|b-3|=0,
+|b-3|=0,
∴a+1=0,b-3=0,解得a=-1,b=3,
∵A(0,3),B(-1,0);
(2)∵B(-1,0),D(2,0),A(0,3),
∴OB=1,OD=2,即BD=OB+OD=1+2=3,
∴OA=BD=3,
在△ABO和△BED中,
∠AOB=∠BDE=90°,
∠ABO=∠BEO,
OA=BD,
∴△ABO≌△BED(AAS),
∴ED=OB=1,
∴E(2,1).
(2)如图所示,当∠BAF=90°时,
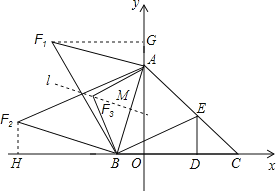
过点F1作F1G⊥y轴于点G,
∵∠F1AG+∠AF1G=90°,∠F1AG+∠BAO=90°,
∴∠AF1G=∠BAO,
在△AGF1与△BOA中,
∠AF1G=∠BAO,
∠AGF1=∠BOA,
AF1=AB,
∴△AGF1≌△BOA,
∴AG=OB=1,GF1=OA=3,
∴F1(-3,4);
当∠ABF=90°时,过点F2作F2G⊥x轴于点H,
同理可得△OAB≌△HBF2,
∴BH=OA=3,F2H=OB=1,
∴OH=BH+OB=3+1=4,
∴F2(-4,1);
当∠AFB=90°时,设直线AB的解析式为y=kx+b(k≠0),
∵A(0,3),B(-1,0),
∴![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=3x+3.
设线段AB的中点为M,则M(-![]() ,
,![]() ),
),
设线段AB的垂直平分线l的解析式为y=-![]() x+c(a≠0),
x+c(a≠0),
∴![]() +c=
+c=![]() ,解得c=
,解得c=![]() ,
,
∴直线l的解析式为y=-![]() x+
x+![]() .
.
设F3(x,-![]() x+
x+![]() ),
),
∵△AF3B是等腰直角三角形,AB=![]() =
=![]() ,
,
∴AF3=![]() ,
,
∴x2+(-![]() x+
x+![]() -3)2=5,解得x=-1,
-3)2=5,解得x=-1,
∴F3(-1,2).
综上所述,F点的坐标为(-3,4)或(-4,1)或(-1,2).

 名校课堂系列答案
名校课堂系列答案