��Ŀ����
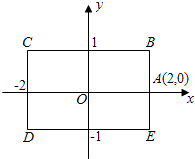
����Ŀ����ͼ��������OABC�У�OΪƽ��ֱ������ϵ��ԭ�㣬A�������Ϊ��4��0����C�������Ϊ��0��6������B�ڵ�һ�����ڣ���P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O��C��B��A��O��·���ƶ����������ų������ƶ�һ�ܣ��� 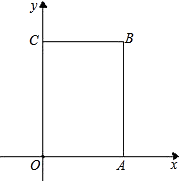
��1��д��B������꣨����
��2������P�ƶ���4��ʱ�������ʱP���λ�ã���д����P�����꣮
��3�����ƶ������У�����P��x�����Ϊ5����λ����ʱ�����P�ƶ���ʱ�䣮
���𰸡�
��1��4��6
��2���⣺��ͼ��ʾ��
�ߵ�P�ƶ���4��ʱ�ľ�����2��4=8��
���P��������2��6����
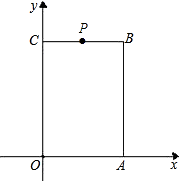
��3���⣺��P��x�����Ϊ5����λ����ʱ����P��������Ϊ5��
����P��OC�ϣ���OP=5��
t=5��2=2.5�룬
����P��AB�ϣ���OP=OC+BC+BP=6+4+��6��5��=11��
t=11��2=5.5�룬
������������P�ƶ���ʱ��Ϊ2.5���5.5��
���������⣺��1����A�������Ϊ��4��0����C�������Ϊ��0��6���� ��OA=4��OC=6��
���B��4��6����
�ʴ�Ϊ��4��6��
��1�����ݾ��ε������Լ��������Ķ���д�����ɣ���2������õ�P�˶��ľ��룬�Ӷ��ɵõ���P�����ꣻ��3�����ݾ��ε������Լ��㵽x��ľ������������ij������OP���ٸ���ʱ��=·�̡��ٶ���ʽ���㼴�ɵý⣮

 ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д�