题目内容
【题目】我们知道平行四边形有很多性质，现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论．
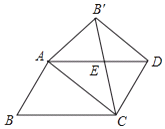
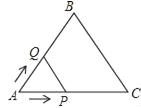
（发现与证明）ABCD中，AB≠BC，将△ABC沿AC翻折至△AB`C，连结B`D．
结论1：△AB`C与ABCD重叠部分的图形是等腰三角形；结论2：B`D∥AC；
（1）请证明结论1和结论2；
（应用与探究）
（2）在ABCD中，已知BC=2，∠B=45°，将△ABC沿AC翻折至△AB`C，连接B`D
若以A、C、D、B`为顶点的四边形是正方形，求AC的长（要求画出图形）
【答案】【发现与证明】（1）见解析；【应用与探究】（2）AC的长为
或2．
【解析】
结论1：先判断出
，进而判断出
，即可得出结论；
结论2、先判断出
，进而判断出
，再判断出
，即可得出结论；
分两种情况：利用等腰直角三角形的性质即可得出结论．
解：结论1：
四边形ABCD是平行四边形，
，
，
，
由折叠知，
≌
，
∴∠ACB=∠ACB’,BC=B’C
∴∠EAC=∠ACB’
，
即
是等腰三角形；
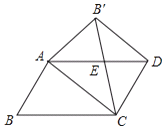
结论2：由折叠知，
，
，
∵AE=CE
【应用与探究】：分两种情况：
如图1所示：
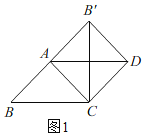
四边形
是正方形，
，
，
，
；
如图2所示：
；
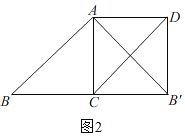
综上所述：AC的长为或2．
练习册系列答案
名校课堂系列答案
相关题目
