题目内容
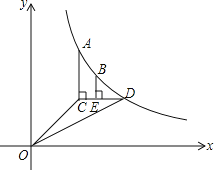
【题目】如图,抛物线y=﹣(x+1)(x﹣m)交x轴于A,B两点(A在B的左侧,m>0),交y轴正半轴于点C,过点C作x轴的平行线交抛物线于另一点E,抛物线的对称轴交CE于点F,以C为圆心画圆,使⊙C经过点(0,2).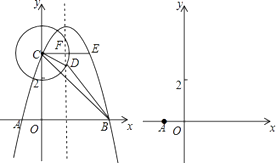
(1)直接写出OB,OC的长.(均用含m的代数式表示)
(2)当m>2时,判断点E与⊙C的位置关系,并说明理由.
(3)当抛物线的对称轴与⊙C相交时,其中下方的交点为D.连结CD,BD,BC.
①当m>3,且C,D,B三点在同一直线上时,求m的值.
②当△BCD是以CD为腰的等腰三角形时,求m的值.(直接写出答案即可)
【答案】
(1)
解:由抛物线y=﹣(x+1)(x﹣m)可知A(﹣1,0),B(m,0),
∴OB=m,
令x=0,求得y=m,
∴C(0,m),
∴OC=m
(2)
解:∵OA=1,OB=m,
∴CE=m﹣1,
∵⊙C经过点(0,2),
∴⊙C的半径为m﹣2,
∵m﹣2<m﹣1,
∴点E在⊙C外
(3)
解:①∵OB=OC=m,
∴△BOC是等腰直角三角形,
∴∠OCB=45°,
∴∠BCE=45°,
∵C,D,B三点在同一直线上,
∴△CDF是等腰直角三角形,
∴CD= ![]() CF,即m﹣2=
CF,即m﹣2= ![]()
![]() ,
,
解得m=3+ ![]() ;
;
②∵CD=m﹣2,CF= ![]() ,
,
∴FD= ![]() =
= ![]() ,
,
∴D( ![]() ,m﹣
,m﹣ ![]() ),
),
∵△BCD是以CD为腰的等腰三角形,
∴D在直线BC的垂直平分线上,
∵OB=OC=m,
∴直线BC的垂直平分线为y=x,
把D( ![]() ,m﹣
,m﹣ ![]() )代入得,
)代入得, ![]() =m﹣
=m﹣ ![]() ,
,
整理得m2﹣8m+7=0,解得m1=1,m2=7,
∴当△BCD是以CD为腰的等腰三角形时,m的值为1或7
【解析】(1)由抛物线y=﹣(x+1)(x﹣m)可知A(﹣1,0),B(m,0),得出OB=m,令x=0,求得y=m,得出OC=m;(2)根据抛物线的对称性求得CE=m﹣1,因为⊙C经过点(0,2),所以⊙C的半径为m﹣2,根据m﹣2<m﹣1,即可判定点E在⊙C外;(3)①先证得△BOC是等腰直角三角形,进而证得△CDF是等腰直角三角形,得出CD= ![]() CF,即m﹣2=
CF,即m﹣2= ![]()
![]() ,解得m=3+
,解得m=3+ ![]() ;②由CD=m﹣2,CF=
;②由CD=m﹣2,CF= ![]() ,根据勾股定理FD=
,根据勾股定理FD= ![]() =
= ![]() ,得出DG=m﹣
,得出DG=m﹣ ![]() ,根据CD=DB,得出D在直线BC的垂直平分线上,根据OB=OC=m,得出直线BC的垂直平分线为y=x,代入D(
,根据CD=DB,得出D在直线BC的垂直平分线上,根据OB=OC=m,得出直线BC的垂直平分线为y=x,代入D( ![]() ,m﹣
,m﹣ ![]() ),整理得出m2﹣8m+7=0,解得m1=1,m2=7.
),整理得出m2﹣8m+7=0,解得m1=1,m2=7.
【考点精析】关于本题考查的二次函数的性质和点和圆的三种位置关系,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;圆和点的位置关系:以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r才能得出正确答案.