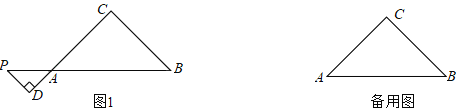题目内容
【题目】如图，线段AB是直线y=x+1的一部分，其中点A在y轴上，点B横坐标为2，曲线BC是双曲线
（
）的一部分，由点C开始不断重复“ABC”的过程，形成一组波浪线，点P(2019，m)与Q(2025，n)均在该波浪线上，G为x轴上一动点，则△PQG周长的最小值为（ ）
A.16B.
C.
D.
【答案】B
【解析】
由点B在直线y=x+1上，点B横坐标为2，可求纵坐标，确定点B的坐标，进而求出反比例函数的关系式，再确定点C的坐标，由点C开始不断重复“A-B-C”的过程，可以推断点P（2019，m）与Q（2025，n）具体所在的位置，再依据对称，求线段的和最小的方法求出答案．
解：当x=2时，y=x+1=2+1=3，
∴B（2，3）
∵B（2，3）在双曲线
上，
∴k=6
把x=6代入
得：y=1，
∴C（6，1）
∵2019÷6=336……3，2025÷6=337……3，
∴点P落在第337个“A-B-C”的P处，
而点Q落在第338个“A-B-C”的Q处，示意如图：
把
代入
P（2019，2），Q（2025，2），
周长的最小，PQ=6定值，
只要GP+GQ最小即可，
过
作
轴，使
关于
轴对称，
连接
交轴于
由勾股定理得：
∴
周长的最小值为PQ+GP+GQ=
故选B．
【题目】已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：
）是反比例函数关系．当
时，
．
（1）写出I关于R的函数解析式；
（2）完成下表，并在给定的平面直角坐标系中画出这个函数的图象；
| … | … | ||||||||
| … | … |
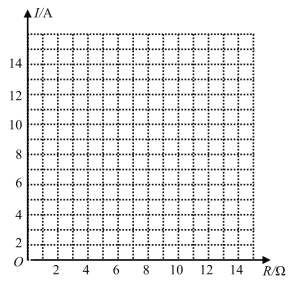
（3）如果以此蓄电池为电源的用电器的限制电流不能超过
．那么用电器可变电阻应控制在什么范围内？
【题目】近几年，国内快递业务快速发展，由于其便捷、高效，人们越来越多地通过快递公司代办点来代寄包裹．某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据（每天代寄包裹数、天数均为整数）统计如下：
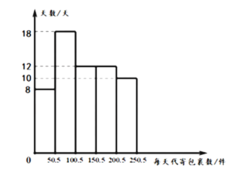
（1）求该数据中每天代寄包裹数在
范围内的天数；
（2）若该代办点对顾客代寄包裹的收费标准为：重量小于或等于1千克的包裹收费8元；重量超1千克的包裹，在收费8元的基础上，每超过1千克（不足1千克的按1千克计算）需再收取2元．
①某顾客到该代办点寄重量为1.6千克的包裹，求该顾客应付多少元费用？
②这60天中，该代办点为顾客代寄的包表中有一部分重量超过2千克，且不超过5千克．现从中随机抽取40件包裹的重量数据作为样本，统计如下：
重量G（单位：千克） |
|
|
|
件数（单位：件） | 15 | 10 | 15 |
求这40件包裹收取费用的平均数．
