题目内容
【题目】如图,在平面直角坐标系中,点A(﹣6,0),点B(0,8),点C在线段AB上,点D在y轴上,将∠ABO沿直线CD翻折,使点B与点A重合.若点E在线段CD延长线上,且CE=5,点M在y轴上,点N在坐标平面内,如果以点C、E、M、N为顶点的四边形是菱形,那么点N有( )
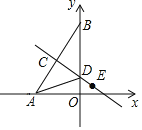
A.2个B.3个C.4个D.5个
【答案】D
【解析】
分别以EC为边,EC为对角线讨论可知满足条件的菱形.
如图,由题意得:AB=![]() ,
,
C为AB的中点,AC=BC=5,
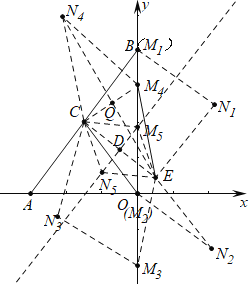
以EC为边时,过点B作BN1∥CE,BN1=CE,则四边形CEN1M1为菱形;
平移CE,当点C落在y轴时(点M2的位置),点E平移到N2的位置,此时四边形CM2N2E为菱形;
平移CE,当点E落在y轴时(点M3的位置),点C平移到N3的位置,此时四边形CN3M3E为菱形;
平移CE,当点E落在y轴时(点M4的位置),点C平移到N4的位置,此时四边形CN4M4E为菱形;
以EC为对角线,作CE的垂直平分线M5N5,交y轴于点M5,作EN5∥CM5且EN5= CM5,连接C、N5,此时四边形CN5EM5为菱形;
综上,可知满足条件的菱形有5个.
故选:D.

练习册系列答案
相关题目