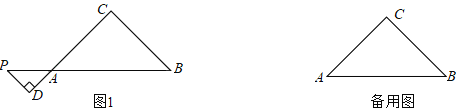题目内容
【题目】如图,直线![]() 与x轴交于A,与y轴交于B,抛物线
与x轴交于A,与y轴交于B,抛物线![]() 经过点A,且与y轴交于点C(0,4),P为x轴上一动点,按逆时针方向作CPE,使CPE∽AOB.
经过点A,且与y轴交于点C(0,4),P为x轴上一动点,按逆时针方向作CPE,使CPE∽AOB.
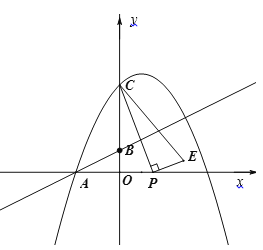
(1)求抛物线解析式.
(2)若点E落在抛物线上,求出点P的坐标.
(3)若ABE是直角三角形,直接写出点P的坐标.
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,0)、 P(
,0)、 P(![]() ,0);(3) P点的坐标为(
,0);(3) P点的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)先根据一次函数![]() 确定A的坐标,然后运用A、C的坐标采用待定系数法解答即可;
确定A的坐标,然后运用A、C的坐标采用待定系数法解答即可;
(2)作EF⊥x轴于F,先求出OA和OB的比值,然后根据△CPE∽△AOB得到![]() ,再证明△CPO∽△PEF,得到
,再证明△CPO∽△PEF,得到![]() ,进一步得到EF=
,进一步得到EF=![]() ;设P(t,0),则E(t+2,
;设P(t,0),则E(t+2,![]() ) ,然后将E的坐标代入解析式求解即可;
) ,然后将E的坐标代入解析式求解即可;
(3)分∠ABE=90°和∠BAE=90°两种情况,分别设设P(a,0)、E(b,c)表示出EF、PF、PG、CG,再证明△EFP∽△PGC得到![]() ,可用a表示出b和c;然后再确定AB2、 BE2、AE2,最后运用勾股定理列方程解答即可.
,可用a表示出b和c;然后再确定AB2、 BE2、AE2,最后运用勾股定理列方程解答即可.
解:(1)直线![]()
当y=0时,x= -2
∴A(-2,0)
把(-2,0) (0,4)代入抛物线中得
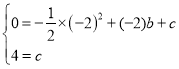 解得:c=4,b=1
解得:c=4,b=1
∴![]() ;
;
(2)作EF⊥x轴于F
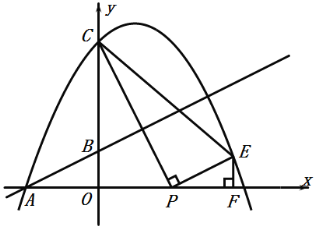
∵直线AB交y轴于点(0,1)
∴![]()
又∵△CPE∽△AOB
∴![]()
又∵∠CPE=90,
∴∠CPO+∠EPF=90
又∠EPF﹢∠PEF=90,
∴∠CPO=∠PEF
∴△CPO∽△PEF
∴![]()
∴PF=2
EF=![]()
设P(t,0)
则E(t+2,![]() )
)
∵E在抛物线上
∴![]()
解得t=![]()
∴P(![]() ,0)、 P(
,0)、 P(![]() ,0);
,0);
(3)①如图:当∠ABE=90°时,设P(a,0),E(b,c)
则EF=a-b,PF=-c,PG=4,CG=a
∵∠GCP+∠GPC=90°,∠EPF+∠GPC=90°
∴∠GCP=∠EPF
∴△EFP∽△PGC
∴![]() ,即
,即![]() ,解得b=a-2,c=
,解得b=a-2,c=![]()
∵直角三角形ABE,
∴AE2=AB2+BE2, AB2=5, BE2=(a-2-0)2+(![]() -1)2,AE2=(a-2+2)2+(
-1)2,AE2=(a-2+2)2+(![]() )2,
)2,
∴5+(a-2)2+(![]() -1)2=a2+(
-1)2=a2+(![]() )2,解得a=
)2,解得a=![]()
∴P的坐标为(![]() ,0);
,0);
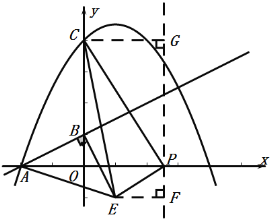
②如图:当∠BAE=90°时,设P(a,0),E(b,c)
则EF=b-a,PF=-c,PG=4,CG=-a
∵∠GCP+∠GPC=90°,∠EPF+∠GPC=90°
∴∠GCP=∠EPF
∴△EFP∽△PGC
∴![]() ,即
,即![]() ,解得b=2+a,c=
,解得b=2+a,c=![]()
∵直角三角形ABE,
∴BE2=AB2+AE2, AB2=5, BE2=(2+a-0)2+(![]() -1)2,AE2=(2+a+2)2+(
-1)2,AE2=(2+a+2)2+(![]() )2,
)2,
∴ ( 2+a)2+(![]() -1)2=(a+4)2+(
-1)2=(a+4)2+(![]() )2+5,解得a=
)2+5,解得a=![]()
∴P的坐标为(![]() ,0).
,0).
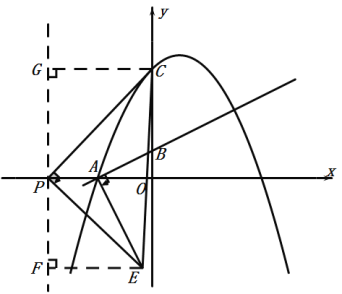
综上,P点的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案【题目】已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:![]() )是反比例函数关系.当
)是反比例函数关系.当![]() 时,
时,![]() .
.
(1)写出I关于R的函数解析式;
(2)完成下表,并在给定的平面直角坐标系中画出这个函数的图象;
| … | … | ||||||||
| … | … |
(3)如果以此蓄电池为电源的用电器的限制电流不能超过![]() .那么用电器可变电阻应控制在什么范围内?
.那么用电器可变电阻应控制在什么范围内?
【题目】近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:
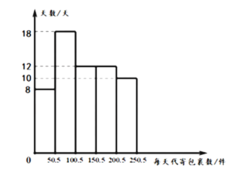
(1)求该数据中每天代寄包裹数在![]() 范围内的天数;
范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
重量G(单位:千克) |
|
|
|
件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.