题目内容
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(![]() ,0),B(
,0),B(![]() ,0),且
,0),且![]() 、
、![]() 满足
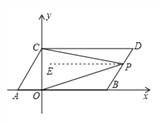
满足![]() ,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.

(1)请直接写出C,D两点的坐标.
(2)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)![]() 的值是否发生变化?并说明理由.
的值是否发生变化?并说明理由.
(3)在坐标轴上是否存在一点M,使三角形MBC的面积与三角形ACD的面积相等?若存在直接写出点M的坐标,若不存在,试说明理由.
【答案】(1)C(0,2) D(4,2)(2) ![]() ,比值不变(3)M点的坐标为(0,
,比值不变(3)M点的坐标为(0, ![]() )或(0,-
)或(0,-![]() )或(7,0)或(-1,0)
)或(7,0)或(-1,0)
【解析】分析:(1)、首先根据非负数的性质得出得出a和b的值,从而得出点A和点B的坐标,然后根据点的平移法则得出点C和点D的坐标;(2)、过点P作PE∥AB,根据平行线的性质得出∠DCP=∠CPE,∠BOP=∠OPE,从而根据角度之间的关系得出答案;(3)、根据等积法得出点M的坐标.
详解:(1)C(0,2) D(4,2)
(2) ![]() ,比值不变,理由如下:
,比值不变,理由如下:
由平移的性质可得CD∥AB, 过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE, ∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP
∴![]()
(3)M点的坐标为(0, ![]() )或(0,-
)或(0,-![]() )或(7,0)或(-1,0)
)或(7,0)或(-1,0)

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目







