题目内容
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).点D在线段PQ上,且PD=PC. 
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长.
【答案】
(1)证明:∵在Rt△ABC中,AB=15,BC=9,
∴AC= ![]() =12,
=12,
∵ ![]() ,
, ![]() ,
,
∴ ![]()
∵∠C=∠C,
∴△PQC∽△BAC,
∴∠CPQ=∠B,
∴PQ∥AB;
(2)解:如图,

连接AD,
∵PQ∥AB,
∴∠ADQ=∠DAB.
∵点D在∠BAC的平分线上,
∴∠DAQ=∠DAB,
∴∠ADQ=∠DAQ,
∴AQ=DQ.
在Rt△CPQ中,PQ=5x,
∵PD=PC=3x,
∴DQ=2x.
∵AQ=12﹣4x,
∴12﹣4x=2x,
解得x=2,
∴CP=3x=6.
【解析】(1)先用勾股定理求出AC,再用两边对应成比例,夹角相等,两三角形相似,得出△PQC∽△BAC,从而有∠CPQ=∠B即可;(2)先判断出AQ=DQ,再用勾股定理AQ,最后建立方程12﹣4x=2x,求解方程即可.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】根据如表回答下列问题:
x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(1)275.56的平方根是______ ;
(2)![]() = ______ ;
= ______ ;
(3)查看上表, <![]() < .
< .
【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
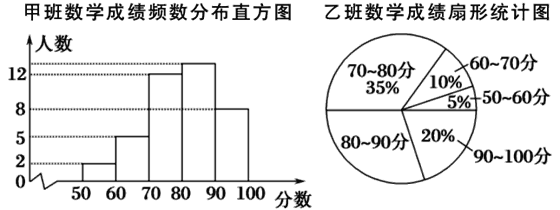
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________