��Ŀ����
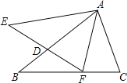
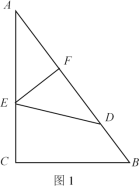
����Ŀ����֪������ֽƬABC�����С�C��90����AB��10��BC��6����E��F�ֱ���AC��AB�ϵĵ㣬����EF��
��1����ͼ1������ֽƬABC��EF�۵����۵����A�պ�����AB���ϵ�D������S��ADE=S�ı���BCED����ED�ij���
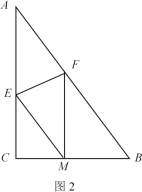
��2����ͼ2������ֽƬABC��EF�۵����۵����A�պ�����BC���ϵ�M������EM��AB��
�����ж��ı���AEMF����״����˵�����ɣ�
�����ۺ�EF�ij���
���𰸡���1��DE��5����2�����ı���AEMF�����Σ�֤������������![]()
��������
��1���������۵������ʵõ�EF��AB����AEF�ա�DEF����S��AEF��S��DEF������S��ABC��5S��AEF����֤��Rt��AEF��Rt��ABC��Ȼ��������������ε����ʵõ���������������Ⱥ�AB��AE�Ĺ�ϵ�������ù��ɶ������AB���ɵõ�AE�ij���
��2���������ı���ȵ��ı���������֤�����ɣ�
����AE��x����EM��x��CE��8x����֤����CME�ס�CBA�õ�����x�ı���ʽ�����x������CM��ֵ�������ù��ɶ��������AM��Ȼ��������ε������ʽ����EF��
��1���ߡ�ACB��һ����EF�۵����۵����A����AB���ϵĵ�D����
��EF��AB����AEF�ա�DEF��
��S��AEF��S��DEF��
��S��ADE��S�ı���BCDE��
��S��ABC��4S��AEF��
��Rt��ABC�У��ߡ�ACB��90![]() ��AB��10��BC��6��
��AB��10��BC��6��
��AC��8��
�ߡ�EAF����BAC��
��Rt��AEF��Rt��ABC��
��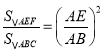 ����
����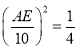 ��
��
��AE��5(��ֵ��ȥ)��
���۵�֪��DE��AE��5��
��2������ͼ2�У��ߡ�ACB��һ����EF�۵����۵����A����BC���ϵĵ�M����
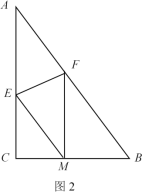
��AE��EM��AF��MF����AFE����MFE��
��ME��AB��
���AFE����FEM
���MFE����FEM��
��ME��MF��
��AE��EM��MF��AF��
���ı���AEMFΪ���Σ�
����AE��x����EM��x��CE��8x��
���ı���AEMFΪ���Σ�
��EM��AB��
���CME�ס�CBA��
��![]() ��
��
��![]() ��
��
���x��![]() ��CM��
��CM��![]() ��
��
��Rt��ACM��AM��![]() ��
��
��S����AEMF��![]() EFAM��AECM��
EFAM��AECM��
��EF��2��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�