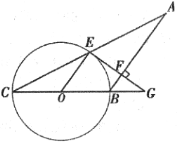
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,连接
上一动点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,当点
折叠,当点![]() 的对应点
的对应点![]() 落在线段
落在线段![]() 的垂直平分线上时,
的垂直平分线上时,![]() 的长等于__________.
的长等于__________.
【答案】![]() 或10.
或10.
【解析】
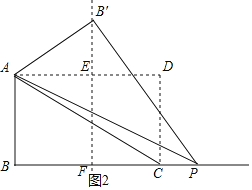
①如图1,当点P在线段BC上时,②如图2,当点P在BC的延长线上时,过A,C分别作AD∥BC,CD∥AB两线交于D,得到四边形ABCD是矩形,求得AD=BC=8,过B′作B′F⊥BC于F,反向延长FB′交AD于E,根据勾股定理即可得到结论.
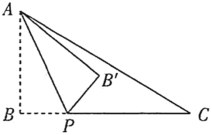
解:①如图1,当点P在线段BC上时,
过A,C分别作AD∥BC,CD∥AB两线交于D, 则四边形ABCD是矩形,
∴AD=BC=8, 过B′作B′F⊥BC于F,反向延长FB′交AD于E, 则AD⊥EF,
∵点B'落在线段BC的垂直平分线上,
∴AE=BF=![]() BC=4,
BC=4,
∵将△ABP沿AP折叠得到△AB′P,
∴AB′=AB=5,PB=PB′,
∴EB′=3, ∴B′F=2,
∴PF=4-PB,
∵![]() ,
,
∴![]() ,
,
解得:![]()
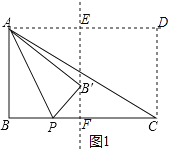
②如图2,当点P在BC的延长线上时, 过A,C分别作AD∥BC,CD∥AB两线交于D, 则四边形ABCD是矩形,
∴AD=BC=8, 过B′作B′F⊥BC于F,反向延长FB′交AD于E, 则AD⊥EF,
∵点B'落在线段BC的垂直平分线上,
∴AE=BF=![]() BC=4,
BC=4,
∵将△ABP沿AP折叠得到△AB′P,
∴AB′=AB=5,PB=PB′,
∴EB′=3, ∴B′F=8,
∴PF=PB-4,
∵![]() ,
,
∴![]()
解得:BP=10;
综上所述,BP的长等于![]() 或10,
或10,
故答案为: ![]() 或10.
或10.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元. (两种方式每次进园均指单人)
元. (两种方式每次进园均指单人)
设进园次数为![]() (
(![]() 为非负整数)
为非负整数)
![]() 根据题意,填写下表:
根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) | 200 |
![]() 设方式一收费
设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 当
当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
【题目】小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到下表数据:
x | 0.5 | 1 | 1.5 | 2 | 3 | 4 | 6 | 12 |
y | 12 | 6 | ■ | 3 | 2 | 1.5 | 1 | 0.5 |
结果发现一个数据被墨水涂黑了.
(1)被墨水涂黑的数据为_________;
(2)y与x的函数关系式为_________,且y随x的增大而_________;
(3)如图是小亮画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形![]() 的面积记为
的面积记为![]() ,矩形
,矩形![]() 的面积记为
的面积记为![]() ,请判断
,请判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
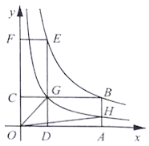
(4)在(3)的条件下,![]() 交
交![]() 于点G,反比例函数
于点G,反比例函数![]() 的图象经过点G交
的图象经过点G交![]() 于点H,连接
于点H,连接![]() 、
、![]() ,则四边形
,则四边形![]() 的面积为_________.
的面积为_________.
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) | x60 | x |
售价(元/件) | 200 | 100 |
若用1800元购进甲种商品的件数与用900元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共100件,其中销售甲种商品为a件(a40),设销售完100件甲、乙两种商品的总利润为w元,求w与a之间的函数关系式,并求出w的最小值.