题目内容
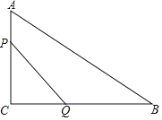
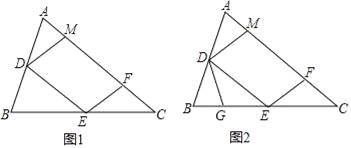
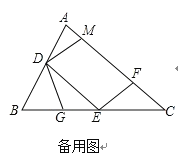
【题目】如图1,在锐角△ABC中,D、E分别是AB、BC的中点,点F在AC上,且满足∠AFE=∠A,DM∥EF交AC于点M.
(1)证明:DM=DA;
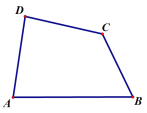
(2)如图2,点G在BE上,且∠BDG=∠C,求证:△DEG∽△ECF;
(3)在图2中,取CE上一点H,使得∠CFH=∠B,若BG=3,求EH的长.
【答案】(1)见解析;(2)见解析;(3)EH= 3.
【解析】
(1)根据平行线性质得∠AMD=∠AFE,可证∠AMD=∠A,得DM=DA;(2)根据三角形中位线性质得DE∥AC,证∠DEG=∠C,∠GDE=∠FEC,可证△DEG∽△ECF;(3)证△BDG∽△BED,得![]() ,BD2=BGBE;证△EFH∽△ECF,得
,BD2=BGBE;证△EFH∽△ECF,得![]() ,EF2=EHEC,又可证四边形DEFM是平行四边形,故EF=DM=DA=BD,所以BGBE=EHEC,又BE=EC,故EH=BG.
,EF2=EHEC,又可证四边形DEFM是平行四边形,故EF=DM=DA=BD,所以BGBE=EHEC,又BE=EC,故EH=BG.
解:(1)证明:如图1所示,
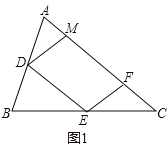
∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:如图2所示,
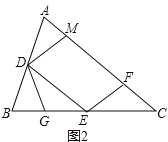
∵D、E分别是AB、BC的中点,
∴DE∥AC,
∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,
∴△DEG∽△ECF;
(3)如图3所示,
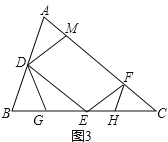
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴![]() ,
,
∴BD2=BGBE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°-∠A-∠B=180°-∠AFE-∠CFH=∠EFH,
又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴![]() ,
,
∴EF2=EHEC,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM=DA=BD,
∴BGBE=EHEC,
∵BE=EC,
∴EH=BG=3.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
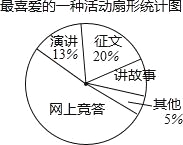
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
人数 | 60 | 30 | 39 | a | b |
(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.