题目内容
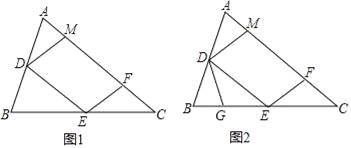
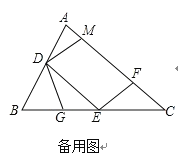
【题目】如图,将边长为6的正方形纸片ABCD沿EF折叠(点E,F分别在边AB,CD上),使点B落在AD边上的点M处(点M不与A,D重),点C落在点N处,MN与CD交于点P, 连接MB,当点M在边AD上移动时.有下列结论:①BM=EF;②0<PF<3 ;③∠AMB=∠BMP;④△PDM的周长随之改变.其中正确结论的序号是_______.(把你认为正确的结论的序号都填上)

【答案】①②③
【解析】
作FG⊥AB于G,证明△ABM≌△GFE(AAS),得出BM=EF,①正确;
若点M与A重合,则C与D重合,P与D重合,PF=3;当M与D重合时,N与C重合,P与C重合,EF与AC重合,CF=0;得出0<PF<3,②正确;
由等腰三角形的性质得出∠ABM=∠EMB,由∠ABC=∠EMN=90°,得出∠AMB=∠BMP,③正确;
可证△AEM∽△DMP,两个三角形的周长的比是AE:MD,设AM=x,根据勾股定理可以用x表示出MD的长与△MAE的周长,根据周长的比等于相似比,求出△PDM的周长=12为定值,得出④不正确,即可得出结论.
解:作FG⊥AB于G,如图所示:
则∠EGF=90°,GF=BC=AB,
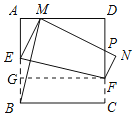
∵四边形ABCD是正方形,
∴∠ABC=∠A=90°,
∴∠ABM+∠AMB=90°,
由折叠的性质得:BM⊥EF,BE=ME,∠EMN=∠ABC=90°,
∴∠ABM+∠GEF=∠ABM+∠AMB=90°,
∴∠AMB=∠GEF,
在△ABM和△GFE中,
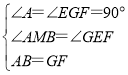 ,
,
∴△ABM≌△GFE(AAS),
∴BM=EF,①正确;
若点M与A重合,则C与D重合,P与D重合,PF=3;
当M与D重合时,N与C重合,P与C重合,EF与AC重合,CF=0;
∵点M不与A,D重合,
∴0<PF<3,②正确;
∵BE=ME,
∴∠ABM=∠EMB,
∵∠ABC=∠EMN=90°,
∴∠AMB=∠BMP,③正确;
设AM=x,则MD=6-x.
由折叠性质可知,EM=BE=6-AE,
在Rt△AEM中,AE2+AM2=EM2,即AE2+x2=(6-AE)2,
整理得:AE2+x2=36-12AE+AE2,
∴AE=![]() (36-x2),
(36-x2),
又∵∠EMP=90°,
∴∠AME+∠DMP=90°.
∵∠AME+∠AEM=90°,
∴∠AEM=∠DMP.
又∵∠A=∠D,
∴△PDM∽△MAE.
∴![]() ,
,
∴△PDM的周长=△MAE的周长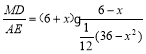 =12.
=12.
∴△PDM的周长保持不变,④不正确;
故答案为:①②③.

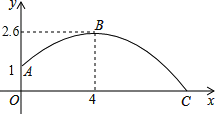
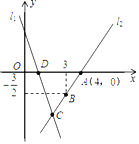
【题目】已知二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | -1 | 0 | m | 8 | … |
(1)可求得m的值为________;
(2)在坐标系画出该函数的图象;
(3)当y≥0时,x的取值范围为_____________

【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?