题目内容
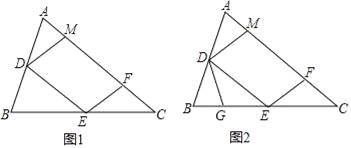
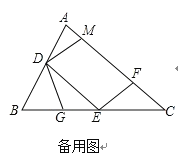
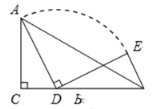
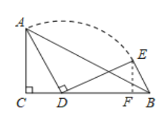
【题目】如图,在△ABC中,∠ACB 90,AC3,CB5,点D是CB边上的一个动点,将线段AD绕着点D 顺时针旋转90,得到线段DE,连结BE,则线段BE的最小值等于__________.
【答案】![]()
【解析】
根据题意过E作EF⊥BC于F,根据余角的性质得到∠DEF=∠ADC,根据全等三角形的性质得到DF=AC=3,EF=CD,设CD=x,根据勾股定理得到BE2=x2+(2-x)2=2(x-1)2+2,即可得到结论.
解:过E作EF⊥BC于F,
∵∠C=∠ADE=90°,
∴∠EFD=∠C=90°,∠FED+∠EDF=90°,∠EDF+∠ADC=90°,
∴∠DEF=∠ADC,
在△EDF和△DAC中,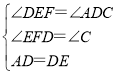 ,
,
∴△EDF≌△DAC(AAS),
∴DF=AC=3,EF=CD,
设CD=x,则BE2=x2+(2-x)2=2(x-1)2+2,
∴BE2的最小值是2,
∴BE的最小值是![]() .
.
故答案为:![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?