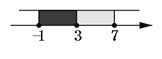ΧβΡΩΡΎ»ί
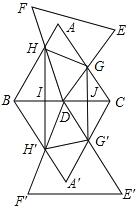
ΓΨΧβΡΩΓΩΘ®12Ζ÷Θ©»γΆΦΘ§÷±Ϋ«»ΐΫ«–ΈΒΡΕΞΒψAΓΔB‘Ύx÷α…œΘ§ABC=90 Θ§BC//y÷αΘ§«“CΒψ‘ΎΒΎΕΰœσœόΘ§BΒψΈΣΘ®-3,0Θ©Θ§ΫΪ÷±Ϋ«»ΐΫ«–ΈABC―Ίx÷αΥ°ΤΫœρ”“ΤΫ“ΤmΗωΒΞΈΜΘ§ΒΟΒΫΕ‘”ΠΒΡ÷±Ϋ«»ΐΫ«–ΈDEFΘ§Τδ÷–ΒψAΓΔBΓΔCΖ÷±πΕ‘”ΠΒψDΓΔEΓΔFΘ§«σΘΚ
Θ®1Θ©”ΟΚ§mΒΡ ΫΉ”±μ ΨEΒψΉχ±ξΦΑADΒΡ≥ΛΕ»ΘΜ
Θ®2Θ©»τCΒψΈΣΘ®-3Θ§nΘ©,…ηΥΡ±Ώ–ΈBEFCΒΡ÷ή≥ΛΈΣyΘ§ ‘”ΟΚ§mΓΔnΒΡ ΫΉ”±μ Ψ÷ή≥ΛyΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§ΒψPΚΆΒψQΖ÷±π“‘1ΗωΒΞΈΜ/ΟκΘ§2ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»Ά§ ±¥”BΒψ≥ωΖΔΘ§Τδ÷–Θ§PΒψ―ΊBΓζCΓζFΓζEΓζBΒΡΖΫœρ‘ΥΕ·Θ§QΒψ―ΊBΓζEΓζFΓζCΓζBΒΡΖΫœρ‘ΥΕ·Θ§œύ”ω ±‘ρΆΘ÷Ι‘ΥΕ·ΓΘΒ±PΒψΒΫ¥οCΒψ ±Θ§QΒψ«ΓΒΫ¥οEΒψΘΜ¥”BΒψ≥ωΖΔΤπΘ§6ΟκΚσPΒψ”κQΒψœύ”ωΆΘ÷ΙΝΥ‘ΥΕ·Θ§«σΥΡ±Ώ–ΈADFCΒΡΟφΜΐΓΘ

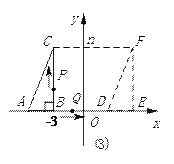
ΓΨ¥πΑΗΓΩ(1) EΒψΈΣΘ®m -3Θ§0Θ©Θ§AD=m;(2) y = 2 m+2 n ΘΜ (3)18
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©”…ΤΫ“ΤΒΡ–‘÷ Φ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
Θ®2Θ©”…ΨΊ–ΈΒΡ–‘÷ ΒΟ≥ωBE=CF=mΘ§BC=EF=nΘ§Φ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
Θ®3Θ©”…Χβ“βΒΟ≥ωmΚΆnΒΡΖΫ≥ΧΉιΘ§ΫβΖΫ≥ΧΉι«σ≥ωmΚΆnΒΡ÷ΒΘ§Φ¥Ω…ΒΟ≥ω¥πΑΗΘ°
‘ΧβΫβΈωΘΚ
Θ®1Θ©ΘΚΘ®1Θ©ΓΏBΘ®-3Θ§0Θ©Θ§
ΓύOB=3Θ§
ΓΏ÷±Ϋ«»ΐΫ«–ΈABC―Ίx÷αΥ°ΤΫœρ”“ΤΫ“ΤmΗωΒΞΈΜΘ§ΒΟΒΫΕ‘”ΠΒΡ÷±Ϋ«»ΐΫ«–ΈDEFΘ§
ΓύAD=BE=mΘ§
ΓύOE=m-3Θ§
ΓύEΒψΈΣΘ®m-3Θ§0Θ©ΘΜ
Θ®2Θ©“Ή÷ΣΘ§ΥΡ±Ώ–ΈBEFCΈΣ≥ΛΖΫ–ΈΘ§BE=CF= mΘ§BC=EF= n
Γύ y = 2 m+2 n
Θ®3Θ©”…Χβ“βΘ§ΒΟΘΚ
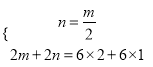
Ϋβ’βΗωΖΫ≥ΧΉιΘ§ΒΟΘΚ
![]()
Γύ![]() Θ§
Θ§ ![]()
”…ΤΫ“Τ÷ΣΘ§ΥΡ±Ώ–ΈADFCΒΡΟφΜΐ=≥ΛΖΫ–ΈBEFCΒΡΟφΜΐ
ΓύΥΡ±Ώ–ΈADFCΒΡΟφΜΐ![]()

 νΦΌœΈΫ”ΫΧ≤ΡΤΎΡ© νΦΌ‘ΛœΑΈδΚΚ≥ωΑφ…γœΒΝ–¥πΑΗ
νΦΌœΈΫ”ΫΧ≤ΡΤΎΡ© νΦΌ‘ΛœΑΈδΚΚ≥ωΑφ…γœΒΝ–¥πΑΗ ΦΌΤΎΉς“Β νΦΌ≥…≥Λά÷‘Α–¬Ϋ°«ύ…ΌΡξ≥ωΑφ…γœΒΝ–¥πΑΗ
ΦΌΤΎΉς“Β νΦΌ≥…≥Λά÷‘Α–¬Ϋ°«ύ…ΌΡξ≥ωΑφ…γœΒΝ–¥πΑΗ