��Ŀ����
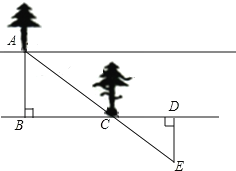
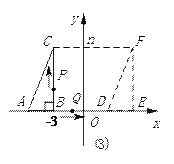
����Ŀ����ͼ����ABC����DEF���DZ߳�Ϊ4�ĵȱ������Σ���DEF�Ķ���DΪ��ABC��һ��BC���е㣬��DEF�Ƶ�D��ת���ұ�DF��DEʼ�շֱ���ABC�ı�AB��AC�ڵ�H��G.ͼ��ֱ��BC�����ͼ�ι���ֱ��BC����Գ�.����HH����HG��GG����H��G��������HH����GG���ֱ�BC�ڵ�I��J.
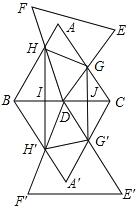
��1����֤����DHB�ס�GDC��
��2����CG=x���ı���HH��G��G�����Ϊy��
����y����x�ĺ�������ʽ���Ա���x��ȡֵ��Χ��
����xΪ��ֵʱ��y��ֵ������ֵΪ���٣�
���𰸡���1��֤������������2����y=![]() ��
��![]() +
+![]() x����4-
x����4-![]() -
-![]() ����1��x��4������x=2��y���=4
����1��x��4������x=2��y���=4![]() .
.
��������
��������������Ǽ��α任�ۺ��⣬��Ҫ�������������ε����ʺ��ж��Լ��ԳƵ����ʣ���x��ʾ�߶��ǽ������Ĺؼ���Ҳ���ѵ㣮
��1���ɵȱ������ε��ص�õ���ȹ�ϵ�����ɣ�
��2�������������εõ�![]() =
=![]() ���ٽ�϶Գƣ���ʾ����ص��߶Σ��ı���HH��G��G�����Ϊy������ɣ�
���ٽ�϶Գƣ���ʾ����ص��߶Σ��ı���HH��G��G�����Ϊy������ɣ�
�����������1��������ABC����ABC=��ACB=60����
����BHD+��BDH=120����
������DEF����EDF=60����
����GDC+��BDH=120����
����BHD=��GDC��
���DHB�ס�GDC��
��2���١�DΪBC���е�,
��BD=CD=2,
����DHB�ס�GDC,
��![]() =
=![]() ����
����![]() =
=![]() ,
,
��BH=![]() ,
,
��H��H���G��G�����BC�Գƣ�
��HH����BC��GG����BC,
����RT��BHI��BI=![]() BH=
BH=![]() ��HI=
��HI=![]() BH=
BH=![]()
![]() ,
,
��RT��CGJ��CJ=![]() CG=
CG=![]() ��GJ=
��GJ=![]() CG=
CG=![]()
![]() ��
��
��HH��=2HI=![]() ��GG��=2GJ=
��GG��=2GJ=![]() x��IJ=4-
x��IJ=4-![]() -
-![]() ,
,
��y=![]() ��
��![]() +
+![]() x����4-
x����4-![]() -
-![]() ����1��x��4��,
����1��x��4��,
�������ã�y=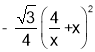 +2
+2![]() ��
��![]() +x��,
+x��,
��![]() +x=a����y=-
+x=a����y=-![]() a2+2
a2+2![]() a,
a,
��a=4ʱ��y���=4![]() ,
,
��ʱ![]() +x=4�����x=2.
+x=4�����x=2.

 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д� ����������������ϵ�д�
����������������ϵ�д�