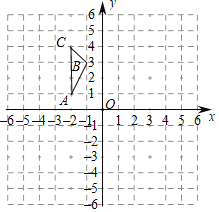题目内容
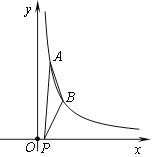
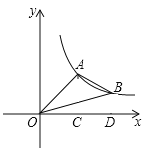
【题目】如图1,点A(8,1)、B(n,8)都在反比例函数![]() (x>0)的图象上,过点A作AC⊥x轴于C,过点B作BD⊥y轴于D.
(x>0)的图象上,过点A作AC⊥x轴于C,过点B作BD⊥y轴于D.
(1)求m的值和直线AB的函数关系式;
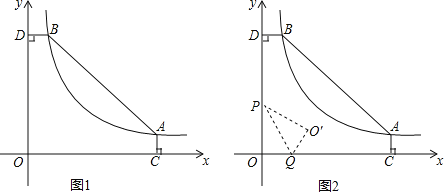
(2)动点P从O点出发,以每秒2个单位长度的速度沿折线OD﹣DB向B点运动,同时动点Q从O点出发,以每秒1个单位长度的速度沿折线OC向C点运动,当动点P运动到D时,点Q也停止运动,设运动的时间为t秒.
①设△OPQ的面积为S,写出S与t的函数关系式;
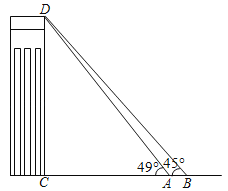
②如图2,当的P在线段OD上运动时,如果作△OPQ关于直线PQ的对称图形△O′PQ,是否存在某时刻t,使得点Q′恰好落在反比例函数的图象上?若存在,求Q′的坐标和t的值;若不存在,请说明理由.
【答案】(1)y=﹣x+9;(2)①S=t2(0<t≤4);S=4t(4<t≤4.5);②![]() .
.
【解析】
(1)由于点A(8,1)、B(n,8)都在反比例函数![]() 的图象上,根据反比例函数的意义求出m,n,再由待定系数法求出直线AB的解析式;
的图象上,根据反比例函数的意义求出m,n,再由待定系数法求出直线AB的解析式;
(2)①由题意知:OP=2t,OQ=t,由三角形的面积公式可求出解析式;
②通过三角形相似,用t的代数式表示出O′的坐标,根据反比例函数的意义可求出t值.
解:(1)∵点A(8,1)、B(n,8)都在反比例函数![]() 的图象上,
的图象上,
∴m=8×1=8,∴y=![]() ,∴8=
,∴8=![]() ,即n=1,
,即n=1,
设AB的解析式为y=kx+b,
把(8,1)、B(1,8)代入上式得:
![]() ,
,
解得:![]() .
.
∴直线AB的解析式为y=﹣x+9;
(2)①由题意知:OP=2t,OQ=t,
当P在OD上运动时,
S=![]() (0<t≤4),
(0<t≤4),
当P在DB上运动时,
S=![]() (4<t≤4.5);
(4<t≤4.5);
②存在,
作PE⊥y轴,O′F⊥x轴于F,交PE于E,
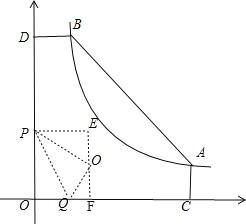
则∠E=90°,PO′=PO=2t,QO′=QO=t,
由题意知:∠PO′Q=∠POQ=90°﹣∠PO′E,
∠EPO′=90′﹣∠PO′E
∴△PEO′∽△O′FQ,
∴![]() ,
,
设QF=b,O′F=a,
则PE=OF=t+b,O′E=2t﹣a,
∴![]() ,
,
解得:a=![]() ,b=
,b=![]() ,
,
∴O′(![]() ,
,![]() ),
),
当Q′在反比例函数的图象上时,
![]() ,
,
解得:t=±![]() ,
,
∵反比例函数的图形在第一象限,
∴t>0,
∴t=![]() .
.
当t=![]() 个长度单位时,Q′恰好落在反比例函数的图象上.
个长度单位时,Q′恰好落在反比例函数的图象上.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案