题目内容
【题目】如图，在矩形ABCD中，CD＝2，AD＝4，点P在BC上，将△ABP沿AP折叠，点B恰好落在对角线AC上的E点．O为AC上一点，⊙O经过点A，P．
（1）求证：BC是⊙O的切线；
（2）在边CB上截取CF＝CE，点F是线段BC的黄金分割点吗？请说明理由．
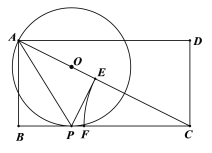
【答案】（1）见解析；（2）点F是线段BC的黄金分割点，理由见解析
【解析】
（1）因为是折叠，可得∠BAP=∠OAP，进而推导出AB∥OP，从而证垂直而得到切线；
（2）在Rt△ABC中，得出AC的长，在根据几何关系，可分别求出CF、BF的长度，得其比值为黄金比例
（1）证明：如图，连接OP，则OA=OP
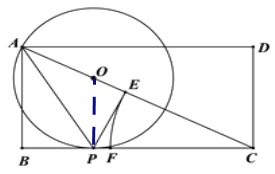
∴∠OAP=∠OPA．
由折叠知∠BAP=∠OAP，∴∠OPA=∠BAP． ∴AB∥OP．
又∵AB⊥BC，∴OP⊥BC．
∴BC是⊙O的切线．
（2）点F是线段BC的黄金分割点，理由如下：
在矩形ABCD中，∵AB=CD＝2，BC=AD＝4，
∴AC=
又∵AE=AB＝2，∴CE=CF＝2
－2．
∴BF=BC－CF=6－2
∵CF2=（2－2）2=24－8 ，
BFBC=4（6－2）=24－8 ，
∴CF2=BFBC．
∴点F是线段BC的黄金分割点．
练习册系列答案
相关题目
