题目内容
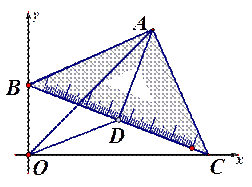
如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧。
(1) 取BC中点D,问OD+DA是否发生改变,若会,说明理由;若不会,求出OD+DA;(2分。)
(2) 你认为OA的长度是否会发生变化?若变化,那么OA最长是多少?OA最长时四边形OBAC是怎样的四边形?并说明理由;(4分。)
(3) 填空:当OA最长时A的坐标*( , ),直线OA的解析式 。(2分。)

图① 图②备用
(1) 取BC中点D,问OD+DA是否发生改变,若会,说明理由;若不会,求出OD+DA;(2分。)
(2) 你认为OA的长度是否会发生变化?若变化,那么OA最长是多少?OA最长时四边形OBAC是怎样的四边形?并说明理由;(4分。)
(3) 填空:当OA最长时A的坐标*( , ),直线OA的解析式 。(2分。)


图① 图②备用
(1)OD+DA=2
(2)因为OD=DA=1始终不变,所以当O、D、A三点在一直线上时,OA最长等于2,这时,四边形OBAC的对角线相交于点D,有DO=DB=DA=DC=1,OA=BC=2,所以四边形OBAC是矩形,因为AB=AC,所以它是正方形。(其他说法,比如可以说明对角线互相垂直平分且相等也可以的。)
(3) A(
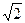 ,
,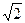 ) y=x。
) y=x。 略

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目


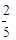
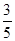
 个细胞,经过第一周期后,在第1 个周期内要死
个细胞,经过第一周期后,在第1 个周期内要死 去1个,会新繁殖(
去1个,会新繁殖(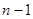 )个;经过第二周期后,在第2 个周期内要死去2个,又会新繁殖(
)个;经过第二周期后,在第2 个周期内要死去2个,又会新繁殖(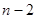 )个;以此类推.例如, 细胞经过第
)个;以此类推.例如, 细胞经过第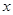 个周期后时
个周期后时 ,在第
,在第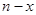 )个.
)个.
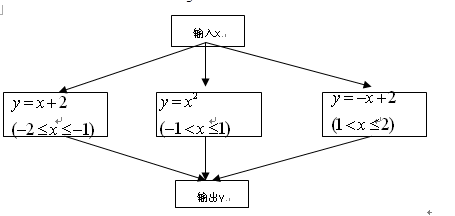
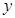 ,则
,则
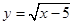 自变量x的取值范围是_______________.
自变量x的取值范围是_______________.
 ON上,O为坐标原点,已知点A的坐标为
ON上,O为坐标原点,已知点A的坐标为 ,正方形ABCD的边长为1.
,正方形ABCD的边长为1. (B)
(B) (C)
(C) (D)
(D)
