题目内容
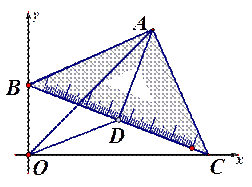
如图,在平面直角坐标系xOy中,O是坐标原点,已知A(3,2)、B(-2,3),则
∠OAB的等于
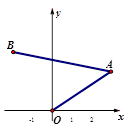
∠OAB的等于
| A.30° | B.45° | C.60° | D.75° |

B
连接OB,根据点的坐标分别求出OB,OA,AB的长,再根据勾股定理的逆定理可得△OAB为等腰直角三角形,根据等腰直角三角形的性质即可求解.
解:连接OB.
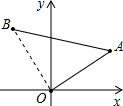
则OA=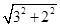 =
=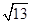 ,OB=
,OB=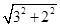 =
=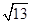 ,AB=
,AB= =
=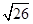 .
.
∵(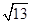 )2+(
)2+(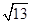 )2=(
)2=(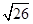 )2,
)2,
∴△OAB为等腰直角三角形,
∴∠OAB=45°.
故选B.
点评:综合性考查了平面直角坐标系两点间的距离公式,勾股定理的逆定理,等腰直角三角形的判定和性质.
解:连接OB.

则OA=
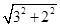 =
=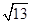 ,OB=
,OB=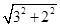 =
=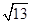 ,AB=
,AB= =
=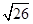 .
.∵(
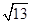 )2+(
)2+(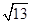 )2=(
)2=(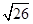 )2,
)2,∴△OAB为等腰直角三角形,
∴∠OAB=45°.
故选B.
点评:综合性考查了平面直角坐标系两点间的距离公式,勾股定理的逆定理,等腰直角三角形的判定和性质.

练习册系列答案
相关题目
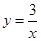 绕着坐标原点旋转90°后,所得到的双曲线的解析式是( )
绕着坐标原点旋转90°后,所得到的双曲线的解析式是( )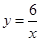
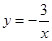
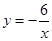
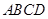 中,
中,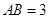 ,
,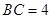 ,点
,点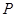 在
在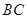 边上
边上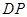 ,过点
,过点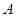 作
作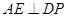 ,垂足为
,垂足为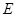 .设
.设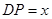 ,
,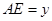 ,则能反映
,则能反映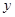 与
与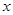 之间函数关系的大致图像( )
之间函数关系的大致图像( ) 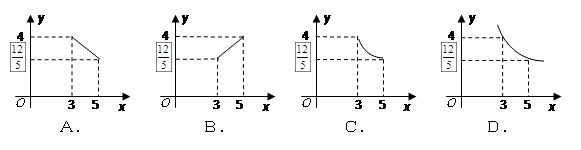


 中,自变量
中,自变量 的取值范围是 .
的取值范围是 .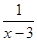
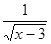
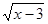
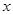 的值为
的值为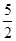 ,则输出的函数值为
,则输出的函数值为 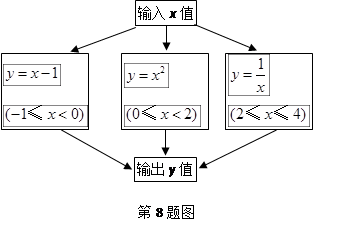
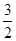
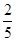
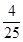

 ).
).