题目内容
【题目】小尧用“描点法”画二次函数![]() 的 图像,列表如下:
的 图像,列表如下:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
y | … | 5 | 0 | -3 | -4 | -3 | 0 | -5 | … |
(1)由于粗心,小尧算错了其中的一个 y值,请你指出这个算错的y值所对应的 x = ;
(2)在图中画出这个二次函数![]() 的图像;
的图像;
(3)当 y≥5 时,x 的取值范围是 .
【答案】(1)2;(2)详见解析;(3)![]() 或
或![]()
【解析】
(1)由表格给出的信息可以看出,该函数的对称轴为直线x=-1,则x=-4与x=2时应取值相同.
(2)将表格中的x,y值看作点的坐标,分别在坐标系中描出这几个点,用平滑曲线连接即可作出这个二次函数的图象;
(3)根据抛物线的对称轴,开口方向,利用二次函数的对称性判断出x=-4或2时,y=5,然后写出y≥5时,x的取值范围即可.
解:(1)从表格可以看出,当x=-2或x=0时,y=-3,
可以判断(-2,-3),(0,-3)是抛物线上的两个对称点,
(-1,-4)就是顶点,设抛物线顶点式y=a(x+1)2-4,
把(0,-3)代入解析式,-3=a-4,解得a=1,
所以,抛物线解析式为y=(x+1)2-4,
当x=-4时,y=(-4+1)2-4=5,
当x=2时,y=(2+1)2-4=5≠-5,
所以这个错算的y值所对应的x=2;
(2)描点、连线,如图:
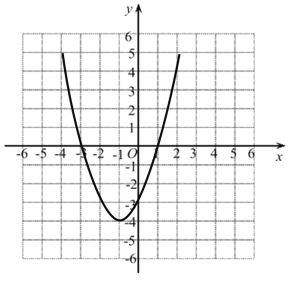
(3)∵函数开口向上,
当y=5时,x=-4或2,
∴当 y≥5 时,由图像可得:
x≤-4或x≥2.

【题目】如图,P是半圆弧![]() 上一动点,连接PA、PB,过圆心O作
上一动点,连接PA、PB,过圆心O作![]() 交PA于点C,连接
交PA于点C,连接![]() 已知
已知![]() ,设O,C两点间的距离为xcm,B,C两点间的距离为ycm.
,设O,C两点间的距离为xcm,B,C两点间的距离为ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是小东的探究过程,请补充完整:
![]() 通过取点、画图、测量,得到了x与y的几组值,如下表:
通过取点、画图、测量,得到了x与y的几组值,如下表:
| 0 |
| 1 |
| 2 |
| 3 |
| 3 |
|
|
|
| 6 |
![]() 说明:补全表格时相关数据保留一位小数
说明:补全表格时相关数据保留一位小数![]()
![]() 建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
![]() 结合画出的函数图象,解决问题:直接写出
结合画出的函数图象,解决问题:直接写出![]() 周长C的取值范围是______.
周长C的取值范围是______.