题目内容
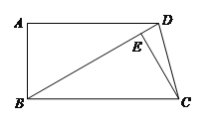
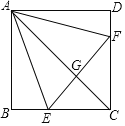
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G.下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,S△ABE=![]() S△CEF.其中正确的是( )
S△CEF.其中正确的是( )
A. ①③B. ②④C. ①③④D. ②③④
【答案】C
【解析】
①通过条件可以得出△ABE≌△ADF,从而得出∠BAE=∠DAF,BE=DF,由正方形的性质就可以得出EC=FC,就可以得出AC垂直平分EF,
②设BC=x,CE=y,由勾股定理就可以得出EF与x、y的关系,表示出BE与EF,即可判断BE+DF与EF关系不确定;
③当∠DAF=15°时,可计算出∠EAF=60°,即可判断△EAF为等边三角形,
④当∠EAF=60°时,设EC=x,BE=y,由勾股定理就可以得出x与y的关系,表示出BE与EF,利用三角形的面积公式分别表示出S△CEF和S△ABE,再通过比较大小就可以得出结论.
①四边形ABCD是正方形,
∴AB═AD,∠B=∠D=90°.
在Rt△ABE和Rt△ADF中,
![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF
∵BC=CD,
∴BC-BE=CD-DF,即CE=CF,
∵AE=AF,
∴AC垂直平分EF.(故①正确).
②设BC=a,CE=y,
∴BE+DF=2(a-y)
EF=![]() y,
y,
∴BE+DF与EF关系不确定,只有当y=(2![]() )a时成立,(故②错误).
)a时成立,(故②错误).
③当∠DAF=15°时,
∵Rt△ABE≌Rt△ADF,
∴∠DAF=∠BAE=15°,
∴∠EAF=90°-2×15°=60°,
又∵AE=AF
∴△AEF为等边三角形.(故③正确).
④当∠EAF=60°时,设EC=x,BE=y,由勾股定理就可以得出:
(x+y)2+y2=(![]() x)2
x)2
∴x2=2y(x+y)
∵S△CEF=![]() x2,S△ABE=
x2,S△ABE=![]() y(x+y),
y(x+y),
∴S△ABE=![]() S△CEF.(故④正确).
S△CEF.(故④正确).
综上所述,正确的有①③④,
故选C.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】小尧用“描点法”画二次函数![]() 的 图像,列表如下:
的 图像,列表如下:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
y | … | 5 | 0 | -3 | -4 | -3 | 0 | -5 | … |
(1)由于粗心,小尧算错了其中的一个 y值,请你指出这个算错的y值所对应的 x = ;
(2)在图中画出这个二次函数![]() 的图像;
的图像;
(3)当 y≥5 时,x 的取值范围是 .