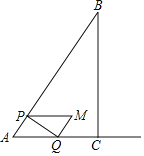题目内容
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ;点
;点![]() 是以
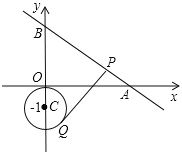
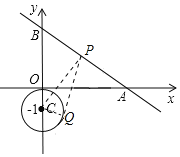
是以![]() 为圆心,1为半径的圆上一动点,过Q点的切线交线段AB于点P,当线段PQ取最小值时,P点的坐标是__________.
为圆心,1为半径的圆上一动点,过Q点的切线交线段AB于点P,当线段PQ取最小值时,P点的坐标是__________.
【答案】![]()
【解析】
先判断当线段PQ取到最小值时的情形:过点C作CP⊥AB与点P,过点P作⊙C的切线PQ,切点为Q,此时PQ取到最小值.根据互相垂直的两条直线的解析式中k互为负倒数,可设直线CP的解析式为:![]() ,把点C(0,-1)代入
,把点C(0,-1)代入![]() 中,求出解析式,再联立直线CP和直线AB这两个函数解析式,求出点P的坐标即可.本题也可用相似三角形结合勾股定理来求点P的坐标.
中,求出解析式,再联立直线CP和直线AB这两个函数解析式,求出点P的坐标即可.本题也可用相似三角形结合勾股定理来求点P的坐标.
解:如下图,过点C作CP⊥AB与点P,过点P作⊙C的切线PQ,切点为Q,此时PQ取到最小值,连接CQ,
∵直线![]()
当x=0时,y=3;当y=0时,x=4,
∴点B的坐标为(0,3),点A的坐标为(4,0),
∵直线CP⊥直线AB,
∴设直线CP的解析式为:![]() ,
,
把点C(0,-1)代入![]() 中,
中,
解得:b=-1,
∴直线CP的解析式为:![]() ,
,
∵直线CP与直线AB交于点P,
∴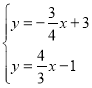 ,
,
解得: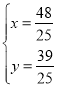 ,
,
∴点P的坐标为![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目