Question

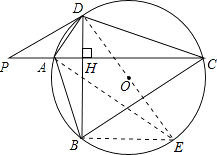
【题目】如图，⊙O的半径r=25，四边形ABCD内接于圆⊙O，AC⊥BD于点H，P为CA延长线上的一点，且∠PDA=∠ABD．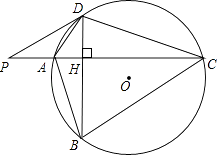
（1）试判断PD与⊙O的位置关系，并说明理由；
（2）若tan∠ADB= ，PA= AH，求BD的长；
（3）在（2）的条件下，求四边形ABCD的面积．

Answer 1

【答案】
（1）解：PD与圆O相切．

理由：如图，连接DO并延长交圆于点E，连接AE，

∵DE是直径，

∴∠DAE=90°，

∴∠AED+∠ADE=90°，

∵∠PDA=∠ABD=∠AED，

∴∠PDA+∠ADE=90°，

即PD⊥DO，

∴PD与圆O相切于点D

（2）解：∵tan∠ADB=

∴可设AH=3k，则DH=4k，

∵PA= AH，

∴PA=（4 ﹣3）k，

∴PH=4 k，

∴在Rt△PDH中，tan∠P= = ，

∴∠P=30°，∠PDH=60°，

∵PD⊥DO，

∴∠BDE=90°﹣∠PDH=30°，

连接BE，则∠DBE=90°，DE=2r=50，

∴BD=DEcos30°= ；

（3）解：由（2）知，BH= ﹣4k，

∴HC= （ ﹣4k），

又∵PD2=PA×PC，

∴（8k）2=（4 ﹣3）k×[4 k+ （25 ﹣4k）]，

解得：k=4 ﹣3，

∴AC=3k+ （25 ﹣4k）=24 +7，

∴S四边形ABCD= BDAC= ×25 ×（24 +7）=900+ ．

【解析】（1）首先连接DO并延长交圆于点E，连接AE，由DE是直径，可得∠DAE的度数，又由∠PDA=∠ABD=∠E，可证得PD⊥DO，即可得PD与圆O相切于点D；（2）首先由tan∠ADB= ，可设AH=3k，则DH=4k，又由PA= AH，易求得∠P=30°，∠PDH=60°，连接BE，则∠DBE=90°，DE=2r=50，可得BD=DEcos30°= ；（3）由（2）易得HC= （ ﹣4k），又由PD2=PA×PC，可得方程：（8k）2=（4 ﹣3）k×[4 k+ （25 ﹣4k）]，解此方程即可求得AC的长，继而求得四边形ABCD的面积．