题目内容
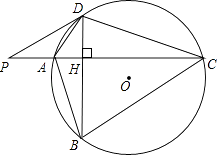
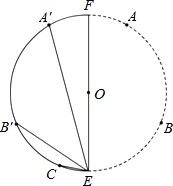
【题目】如图,A,B,C为⊙O上相邻的三个n等分点, ![]() ,点E在
,点E在 ![]() 上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°=
上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°= ![]() ,cos15°=sin75°=
,cos15°=sin75°= ![]() )
)
【答案】c+ ![]() b;c+
b;c+ ![]() b
b
【解析】解:如解答图所示,连接AB、AC、BC. 由题意,点A、B、C为圆上的n等分点,
∴AB=BC,∠ACB= ![]() ×
× ![]() =
= ![]() (度).
(度).
在等腰△ABC中,过顶点B作BN⊥AC于点N,
则AC=2CN=2BCcos∠ACB=2cos ![]() BC,
BC,
∴ ![]() =2cos
=2cos ![]() .
.
连接AE、BE,在AE上取一点D,使ED=EC,连接CD.
∵∠ABC=∠CED,
∴△ABC与△CED为顶角相等的两个等腰三角形,
∴△ABC∽△CED.
∴ ![]() ,∠ACB=∠DCE.
,∠ACB=∠DCE.
∵∠ACB=∠ACD+∠BCD,∠DCE=∠BCE+∠BCD,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
∵ ![]() ,∠ACD=∠BCE,
,∠ACD=∠BCE,
∴△ACD∽△BCE.
∴ ![]() ,
,
∴DA= ![]() EB=2cos
EB=2cos ![]() EB.
EB.
∴EA=ED+DA=EC+2cos ![]() EB.
EB.
由折叠性质可知,p=EA′=EA,b=EB′=EB,c=EC.
∴p=c+2cos ![]() b.
b.
当n=4时,p=c+2cos45°b=c+ ![]() b;
b;
当n=12时,p=c+2cos15°b=c+ ![]() b.
b.
所以答案是:c+ ![]() b,c+
b,c+ ![]() b.
b.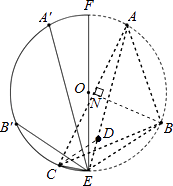

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?