题目内容
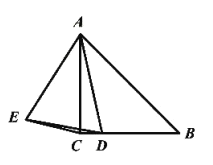
【题目】如图，在
中，
，
，
为
边上一动点，作如图所示的
使得
，且
，连接
，则的最小值为__________．
【答案】
【解析】
根据已知条件，添加辅助线可得△EAC≌△DAM（SAS），进而得出当MD⊥BC时，CE的值最小，转化成求DM的最小值，通过已知值计算即可．
解：如图所示，在AB上取AM=AC=2，
∵
，
，
∴∠CAB=45°，
又∵
，
∴∠EAC+∠CAD=∠DAB+∠CAD=45°，
∴∠EAC =∠DAB，
∴在△EAC与△DAB中
AE=AD，∠EAF =∠DAB，AC =AM，
∴△EAC≌△DAM（SAS）
∴CE=MD，
∴当MD⊥BC时，CE的值最小，
∵AC=BC=2，
由勾股定理可得
，
∴
，
∵∠B=45°，
∴△BDM为等腰直角三角形，
∴DM=BD，
由勾股定理可得
∴DM=BD=
∴CE=DM=
故答案为：
练习册系列答案
相关题目
【题目】A，B两地相距20km．甲、乙两人都由A地去B地，甲骑自行车，平均速度为10km/h；乙乘汽车，平均速度为40km/h，且比甲晚1.5h出发．设甲的骑行时间为x（h）（0≤x≤2）
（1）根据题意，填写下表：
时间x（h） 与A地的距离 | 0.5 | 1.8 | _____ |
甲与A地的距离（km） | 5 |
| 20 |
乙与A地的距离（km） | 0 | 12 |
|
（2）设甲，乙两人与A地的距离为y1（km）和y2（km），写出y1，y2关于x的函数解析式；
（3）设甲，乙两人之间的距离为y，当y=12时，求x的值．
