��Ŀ����
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=13���ף�BC=10���ף�AD��BC�ڵ�D������P�ӵ�A������ÿ��1�����ٶ����߶�AD�����յ�D�˶����趯���˶�ʱ��Ϊt�룮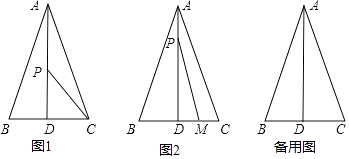
��1����AD�ij���
��2����P��C����ľ���Ϊ ![]() ʱ����t��ֵ��
ʱ����t��ֵ��
��3������M�ӵ�C������ÿ��2�����ٶ�������CB���˶�����M���Pͬʱ�������ҵ���P�˶����յ�Dʱ����MҲֹͣ�˶����Ƿ����ʱ��t��ʹ��S��PMD= ![]() S��ABC�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
S��ABC�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��AB=AC=13��AD��BC��
��BD=CD=5cm���ҡ�ADB=90�㣬
��AD2=AC2��CD2
��AD=12cm
��2��
�⣺AP=t��
��PD=12��t��
��Rt��PDC�У�PC= ![]() ��CD=5�����ݹ��ɶ����ã�PC2=CD2+PD2��
��CD=5�����ݹ��ɶ����ã�PC2=CD2+PD2��
��29=52+��12��t��2��
��t=10��t=14���ᣩ��
����t��ֵΪ10s
��3��
�⣺�������t��ʹ��S��PMD= ![]() S��ABC��
S��ABC��
��BC=10��AD=12��
��S��ABC= ![]() BC��AD=60��
BC��AD=60��
�� ����M���߶�CD�ϣ�
�� 0��t�� ![]() ʱ��PD=12��t��DM=5��2t��
ʱ��PD=12��t��DM=5��2t��
��S��PMD= ![]() S��ABC��
S��ABC��
�� ![]() ��12��t����5��2t��=
��12��t����5��2t��= ![]() ��
��
2t2��29t+43=0
���t1= ![]() ����ȥ����t2=
����ȥ����t2= ![]()
�� ����M������DB�ϣ��� ![]() ��t��12��
��t��12��
��S��PMD= ![]() S��ABC
S��ABC
�� ![]() ��12��t����2t��5��=
��12��t����2t��5��= ![]() ��
��
2t2��29t+77=0
��� t=11��t= ![]()
���ϣ�����t��ֵΪ ![]() s�� 11s��
s�� 11s�� ![]() s��ʹ��S��PMD=
s��ʹ��S��PMD= ![]() S��ABC
S��ABC
����������1�����ݵ������������ʺ��ɶ�����ɣ���2�����ݹ��ɶ�������������⼴�ɣ���3�����������г�PD��MD�ı���ʽ�ⷽ���飬����M��D���������������ͬ�����Խ��зֶ����ۼ��ɣ�ע��Լ��������
�����㾫����������Ĺؼ���������ɶ����ĸ�������֪ʶ������ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��

 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�����Ŀ����20��ײˣ���ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ����¼���£�
��������IJ�ֵ����λ��ǧ�ˣ� |
|
|
|
|
|
|
�� �� | 1 | 4 | 2 | 3 | 2 | 8 |
��1��20��ײ��У����ص�һ��������һ����______ǧ�ˣ�
��2����������Ƚϣ�20��ײ��ܼƳ����������ǧ�ˣ�
��3�����ײ�ÿǧ���ۼ�![]() Ԫ���������20��ײ˿�������Ԫ��
Ԫ���������20��ײ˿�������Ԫ��