题目内容
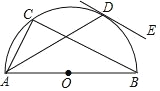
【题目】如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,以AB为直径作⊙O恰好与CD相切.
(1)求证:AD+BC=CD;
(2)若E为OA的中点,连结CE并延长交DA的延长线于F,当AE=AF时,求sin∠DCF.

【答案】(1)详见解析;(2)sin∠DCF=![]() .
.
【解析】
(1)作OH⊥CD于H,如图,根据切线的性质得到点H为切点,再证明AD和BC都与⊙O相切,则根据切线长定理得到DA=DH,CB=CH,于是有AD+BC=DH+CH=CD;
(2)先判断△AEF为等腰直角三角形得到∠F=45°,再判断△OBC为等腰直角三角形得BE=BC,作DG⊥BC于G,如图,易得四边形ABGD为矩形,则设AE=AF=x,AD=y,所以BE=BC=3x,CD=y+3x,DG=4x,CG=CB-BG=3x-y,接着在Rt△DGC中利用勾股定理可计算出y=![]() x,则CD=
x,则CD=![]() x,DF=
x,DF=![]() x;作DK⊥CF于K,如图,则△KDF为等腰直角三角形,于是DK=
x;作DK⊥CF于K,如图,则△KDF为等腰直角三角形,于是DK=![]() DF=
DF=![]() x,然后在Rt△CDK中根据正弦的定义求解.
x,然后在Rt△CDK中根据正弦的定义求解.
(1)证明:作OH⊥CD于H,如图,
∵以AB为直径作⊙O与CD相切,
∴点H为切点,
∵∠ABC=90°,AD∥BC,
∴AD⊥AB,BC⊥AB,
∴AD和BC都与⊙O相切,
∴DA=DH,CB=CH,
∴AD+BC=DH+CH=CD;
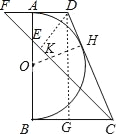
(2)解:∵AE=AF,∠EAF=90°,
∴△AEF为等腰直角三角形,
∴∠F=45°,
∵AF∥BC,
∴∠FCB=45°,
∴△OBC为等腰直角三角形,
∴BE=BC,
作DG⊥BC于G,如图,易得四边形ABGD为矩形,
设AE=AF=x,AD=y,则BE=BC=3x,
∴CD=y+3x,DG=4x,CG=CB﹣BG=3x﹣y,
在Rt△DGC中,∵DG2+CG2=CD2,
∴(4x)2+(3x﹣y)2=(y+3x)2,
∴y=![]() x,
x,
∴CD=![]() x+3x=
x+3x=![]() x,DF=x+
x,DF=x+![]() x=
x=![]() x,
x,
作DK⊥CF于K,如图,则△KDF为等腰直角三角形,
∴DK=![]() DF=
DF=![]() x,
x,
在Rt△CDK中,sin∠DCK=![]() =
=![]() =
=![]() ,
,
即sin∠DCF=![]() .
.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案