题目内容
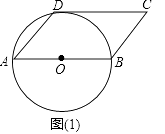
【题目】如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(﹣1,0)C(3,2 ![]() ),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E. 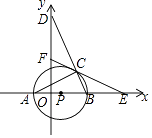
(1)求⊙P的半径;
(2)当∠A=∠DCF时,求证:CE是⊙P的切线.
【答案】
(1)解:作CG⊥x轴于G,
则AC2=AG2+CG2=(3+1)2+(2 ![]() )2=24,
)2=24,
由射影定理得:AC2=AGAB,
∴AB= ![]() =6,
=6,
∴⊙P的半径为3
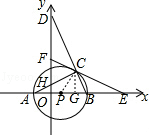
(2)解:证明:连接PC,
∵AB是⊙P的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵PC=PB,
∴∠PCB=∠PBC,
∵∠A=∠DCF=∠ECB,
∴∠ECB+∠PCB=90°,
∵C在⊙P上,
∴CE是⊙P的切线.
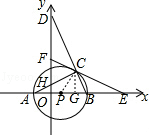
【解析】(1)作CG⊥x轴于G,根据勾股定理和射影定理即可得到结论;(2)连接PC,由AB是⊙P的直径,得到∠ACB=90°根据等腰三角形的性质得到∠PCB=∠PBC,根据切线的判定定理即可得到结论.
【考点精析】通过灵活运用三角形的外接圆与外心和切线的判定定理,掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目