题目内容
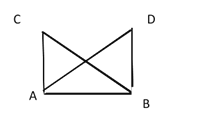
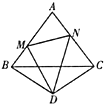
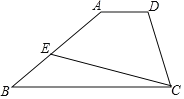
【题目】在四边形ABCD中,AD∥BC,E为AB边上一点,∠BCE=16°,EF∥BC交DC于点F.
(1)依题意补全图形,并求∠FEC的度数;
(2)若∠A=141°,求∠AEC的度数.
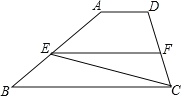
【答案】(1)补全的图形见解析,∠FEC=16°;(2)∠AEC=55°.
【解析】
(1)过点E作∠BEF=∠A交DC于点F,则EF为所求;易证EF∥BC,由平行线的性质即可求出∠FEC的度数;
(2)由平行线的性质可得∠A+∠AEF=180°,则∠AEF的度数可求,进而可求出∠AEC的度数.
(1)补全的图形如图所示.
∵AD∥BC,EF∥AD,
∴EF∥BC,
∴∠FEC=∠BCE.
∵∠BCE=16°,
∴∠FEC=16°.
(2)∵EF∥AD,
∴∠AEF+∠A=180°.
∵∠A=141°,
∴∠AEF=39°,
∴∠AEC=39°+16°=55°.

练习册系列答案
相关题目
【题目】探究函数![]() 的图象与性质.
的图象与性质.
小王根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小亮的探究过程,请你帮忙补充完整:
(1)下表是![]() 与
与![]() 的几组对应值
的几组对应值
| … |
|
|
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
|
|
| … |
则![]() _______;
_______;![]() _______;
_______;
(2)在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
(3)结合函数图象,解决问题:当![]() 时,直接写出所有满足条件的
时,直接写出所有满足条件的![]() 的近似值(精确到
的近似值(精确到![]() ).
).