题目内容
【题目】如图,已知一次函数![]() 的图象分别交
的图象分别交![]() 轴、
轴、![]() 轴于
轴于![]() 、
、![]() 两点,点
两点,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度向点
方向以每秒2个单位长度向点![]() 匀速运动,当其中一点到达终点时,另一点也停止运动,设运动时间为
匀速运动,当其中一点到达终点时,另一点也停止运动,设运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 轴,连接
轴,连接![]() 、
、![]() .
.
(1)点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,
的坐标为________,![]() ________;
________;
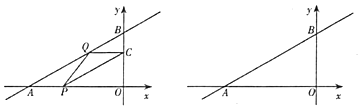
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的值;如果不能,说明理由.
能够成为菱形吗?如果能,求出相应的值;如果不能,说明理由.
(3)若点![]() ,点
,点![]() 在
在![]() 轴上,直线
轴上,直线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请直接写出
为顶点的四边形是平行四边形?若存在,请直接写出![]() 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
【答案】(1)A(6![]() ,0),B(0,6),12;(2)当t=2412
,0),B(0,6),12;(2)当t=2412![]() 时,四边形APCQ为菱形;(3)M点的坐标为(2
时,四边形APCQ为菱形;(3)M点的坐标为(2![]() ,4),(10
,4),(10![]() ,4),(2
,4),(2![]() ,8).
,8).
【解析】
(1)分别令y=0,x=0,即可求得A、B的坐标,然后根据勾股定理即可求得AB的长;
(2)先求得∠BQC=∠BAO=30°,从而得出QC=![]() QB,进而求得QC=
QB,进而求得QC=![]() t,因为AP=
t,因为AP=![]() t,所以四边形APCQ是平行四边形,如果AQ=QC,则四边形APCQ为菱形,根据AQ=QC即可求得;
t,所以四边形APCQ是平行四边形,如果AQ=QC,则四边形APCQ为菱形,根据AQ=QC即可求得;
(3)根据以M、N、B、D为顶点的四边形是平行四边形,可知M点的纵坐标为4,把y=4代入y=![]() x+6即可求得;
x+6即可求得;
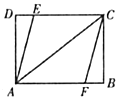
(1)如图1,∵一次函数y=![]() x+6的图象分别交x轴、y轴于A. B两点,
x+6的图象分别交x轴、y轴于A. B两点,
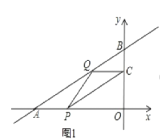
令y=0,则0=![]() x+6,解得:x=6
x+6,解得:x=6![]() ,
,
∴A(6![]() ,0),
,0),
令x=0,则y=6,
∴B(0,6),
∴AB=![]() =12;
=12;
(2)如图1,∵直线AB的斜率为![]() ,
,
∴∠BAO=30°,
∵QC⊥y轴,
∴QC∥x轴,
∴∠BQC=∠BAO=30°,
∴QC=![]() QB,
QB,
∵QB=2t,
∴QC=![]() t,
t,
∵AP=![]() t,
t,
∴四边形APCQ是平行四边形,
∴如果AQ=QC,则四边形APCQ为菱形,
∵AB=12,
∴AQ=122t,
即122t=![]() t,解得:t=2412
t,解得:t=2412![]() ,
,
∴当t=2412![]() 时,四边形APCQ为菱形,
时,四边形APCQ为菱形,
(3)如图2,∵B(0,6),D(0,2),
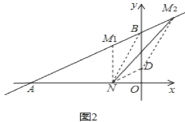
∴BD=4,
当BD是平行四边形的边时,
∵四边形MNDB是平行四边形,
∴MN=BD=4,MN⊥x轴,
把y=4代入y=![]() x+6得:4=
x+6得:4=![]() x+6,
x+6,
解得:x=2![]() ,
,
∴M(2![]() ,4).
,4).
把y=4代入y=![]() x+6得:4=
x+6得:4=![]() x+6,
x+6,
解得:x=10![]() ,
,
M(10![]() ,4),
,4),
当BD是平行四边形的对角线时,
∵BM1=BM2,
∴M的横坐标为2![]() ,
,
代入y=![]() x+6得y=8,
x+6得y=8,
∴M(2![]() ,8),
,8),
故M点的坐标为(2![]() ,4),(10
,4),(10![]() ,4),(2
,4),(2![]() ,8).
,8).

【题目】下列说法正确的有( )
①﹣a一定是负数;
②![]() 一定小于a;
一定小于a;
③互为相反数的两个数的绝对值相等;
④等式﹣a2=|﹣a2|一定成立;
⑤大于﹣3且小于2的所有整数的和是2.
A.0个B.1个C.2个D.3个
【题目】为了满足学生的物质需求,我市某中学到红旗超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该红旗超市有几种进货方案?
(3)在(2)的条件下,该红旗超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?