Question

【题目】如图，二次函数的图像经过，两点.

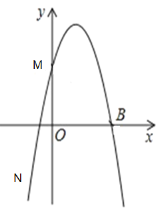
（1）求该函数的解析式；

（2）若该二次函数图像与轴交于、两点，求的面积；

（3）若点在二次函数图像的对称轴上，当周长最短时，求点的坐标.

Answer 1

【答案】（1）；（2）6；（3）

【解析】

（1）将M,N两点代入求出b,c值，即可确定表达式；

（2）令y=0求x的值，即可确定A、B两点的坐标，求线段AB长，由三角形面积公式求解.

（3）求出抛物线的对称轴，确定M关于对称轴的对称点G的坐标，直线NG与对称轴的交点即为所求P点，利用一次函数求出P点坐标.

解：将点，代入中得，

，

解得，，

∴y与x之间的函数关系式为；

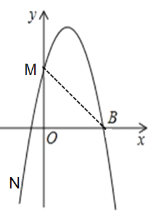
（2）如图，当y=0时，，

∴x1=3,x2= -1,

∴A(-1,0),B(3,0),

∴AB=4,

∴S△ABM= .

即的面积是6.

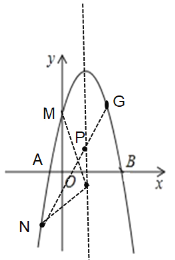
（3）如图，抛物线的对称轴为直线 ，

点关于直线x=1的对称点坐标为G(2，3),

∴PM=PG,

连MG交抛物线对称轴于点P，此时NP+PM=NP+PG最小，即周长最短.

设直线NG的表达式为y=mx+n,

将N(-2,-5),G(2,3)代入得，

，

解得， ，

∴y=2m-1,

∴P点坐标为(1,1).