题目内容
【题目】如图1,已知△ABC和△EFC都是等边三角形,点E在线段AB上. 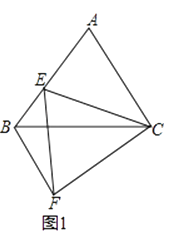
(1)求证:AE=BF,BF∥AC;
(2)若点D在直线AC上,且ED=EC(如图2),求证:AB=AD+BF; 
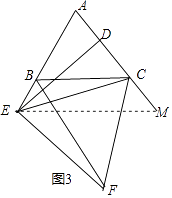
(3)在(2)的条件下,若点E改为在线段AB的延长线上,其它条件不变(如图3),请直接写出AB、AD、BF之间的数量关系. 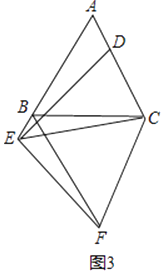
【答案】
(1)解:如图1,∵△ABC和△EFC都是等边三角形,
∴∠ACB=∠ECF=60°,AC=BC,CE=FC,
∴∠1=∠2,
在△ACE和△BCF中,
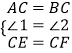 ,
,
∴△ACE≌△BCF(SAS),
∴AE=BF,且∠BAC=∠FBC=60°,
又∠ABC=60°,
∴∠A+∠ABC+∠FBC=180°,即∠A+∠ABF=180°,
∴AC∥BF
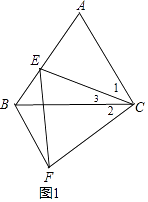
(2)解:证明:如图2,过E作EM∥BC交AC于M,
∵∠ABC=∠ACB=60°,
∴∠AEM=∠AME=60°,
∴△AEM是等边三角形,
∴AE=EM=AM,
∴∠DAE=∠EMC=120°,
∵DE=CE,
∴∠D=∠1,
在△ADE和△MCE中,
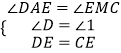 ,
,
∴△ADE≌△MCE(AAS),
∴AD=CM,
由(1)得△ACE≌△FCB,
∴BF=AE=AM,
∵AC=AM+CM,
∴AC=BF+AD,
即AB=BF+AD
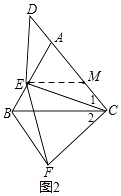
(3)解:AB、AD、BF之间的数量关系为:AB=BF﹣AD,
理由:如图3,过E作EM∥BC交AC的延长线于M,
∵∠ABC=∠ACB=60°,
∴∠AEM=∠AME=60°,
∴△AEM是等边三角形,
∴AE=EM=AM,
∴∠DAE=∠EMC=60°,
∵DE=CE,
∴∠ADE=∠DCE,
∴∠ADE=∠ECM,
在△ADE与△MCE中,
 ,
,
∴△ADE≌△MCE(AAS),
∴AD=CM,
由(1)得△ACE≌△FCB,
∴BF=AE=AM,
∵AM=AC+CM,
∴AC=AM﹣CM,
∴AC=BF﹣AD,
即AB=BF﹣AD.
【解析】(1)根据等边三角形的性质得到∠ACB=∠ECF=60°,AC=BC,CE=FC,推出△ACE≌△FCB,得到AE=BF且∠A=∠CBF=60°,于是得到∠A+∠ABF=180°,根据平行线的判定定理即可得到AC∥BF;(2)过E作EM∥BC交AC于M,得到△AEM是等边三角形,求得AE=EM=AM,∠DAE=∠EMC=120°,根据全等三角形的性质,得到AD=CM,由(1)得△ACE≌△FCB,得到BF=AE,进而推出AB=BF+AD;(3)过E作EM∥BC交AC的延长线于M,推出△AEM是等边三角形,根据等边三角形的性质,得到∠DAE=∠EMC=60°,推出∠ADE=∠ECM,根据全等三角形的性质,得到AD=CM,等量代换即可得到结论.
【考点精析】通过灵活运用平行线的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案