题目内容
【题目】
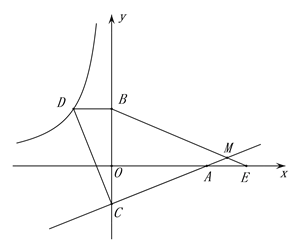
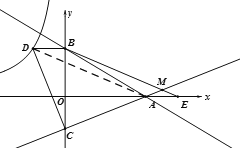
如图,已知点D在反比例函数y=![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=![]() .
.
(1)求反比例函数y=![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
【答案】(1)反比例函数的解析式为: ![]() 一次函数的解析式为:
一次函数的解析式为: ![]() ;
;
(2)![]() ,理由见解析;
,理由见解析;
(3)![]()
【解析】试题分析:(1)由点A(5,0)和tan∠OAC=![]() 可以求出OC=BD的长,一次函数的解析式就可以求出了,继而求出点D的坐标,反比例函数解析式就可以求出了;(2)根据已知条件,得出
可以求出OC=BD的长,一次函数的解析式就可以求出了,继而求出点D的坐标,反比例函数解析式就可以求出了;(2)根据已知条件,得出![]() ,根据等角的余角相等求出垂直关系;(3)连接AD,得出四边形AEBD为平行四边形,求出
,根据等角的余角相等求出垂直关系;(3)连接AD,得出四边形AEBD为平行四边形,求出![]() ,继而求出
,继而求出![]() .
.
试题解析:
(1)∵A(5,0),∴OA=5.
∵![]() ∴
∴![]()
∴![]()
∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
设直线AC关系式为![]() ∵过A(5,0),
∵过A(5,0),![]()
∴![]() 解得:
解得: 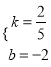 ∴
∴![]() .
.
(2)∵![]() ∴
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ∴
∴,
∴![]()
∴![]() .
.
(3) ![]()
连接AD,
∵![]() ,
, ![]() ∴
∴![]()
∴四边形AEBD为平行四边形,∴![]() ∴
∴![]()
∵![]() ,∴
,∴![]()
∵![]() ∴
∴![]()
∴![]() =45°
=45°

练习册系列答案
相关题目