题目内容
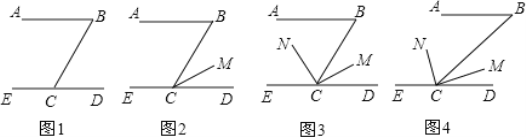
【题目】已知:在△ABC和△DCE中,∠ACB=∠DCE=90°,AC=DC,BC=EC,AB与DE相交于点F.
(1)如图1,求证AB=DE;
(2)如图2,连接CF,求证∠AFC=∠EFC;
(3)如图3,在(2)的条件下,当AF=EF时,连接BD,AE,延长CF交BD于点G,AE交CF于点H,若AE=8,BG=2,求线段GH的长.

【答案】(1)证明见解析;(2)证明见解析;(3)2.
【解析】
(1)证明△ABC≌△DEC(SAS),可得结论;
(2)如图2,作垂线段CM和CN,证明△ACM≌△DCN(AAS),得CM=CN,根据角平分线的逆定理可得:∠AFC=∠EFC;
(3)如图3,先证明△AFC≌△EFC,得AC=EC=BC,再证明△ACH≌△CBG(AAS),得CG和CH的长,利用线段的差可得结论.
证明:(1)如图1,在△ABC和△DEC中,
∵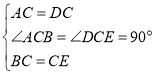 ,
,
∴△ABC≌△DEC(SAS),
∴AB=DE;
(2)如图2,过点C作CM⊥AB,CN⊥DE,垂足分别为M,N,
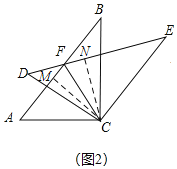
∵△ABC≌△DEC,
∴∠A=∠D,
在△ACM和△DCN中,
∵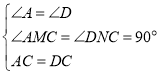 ,
,
∴△ACM≌△DCN(AAS),
∴CM=CN,
∴∠AFC=∠EFC;
(3)如图3,∵AB=DE,AF=EF,
∴AB-AF=DE-EF,即BF=DF,
∵∠AFC=∠EFC,∠AFC=∠BFG,∠EFC=∠DFG,
∴∠BFG=∠DFG,
∴FG⊥BD
∴∠BGF=∠DGF=90°,
同理∠AHF=∠EHF=90°,AH=EH=![]() AE=4,
AE=4,
在△AFC和△EFC中
∵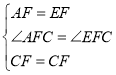
∴△AFC≌△EFC,
∴AC=EC,
∴AC=BC,
∵∠CBG+∠BCG=90°,∠ACH+∠BCG=90°,
∴∠CBG=∠ACH,
在△ACH和△CBG中,
∵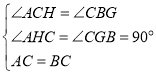 ,
,
∴△ACH≌△CBG(AAS),
∴CH=BG=2,CG=AH=4,
∴GH=CG-CH=4-2=2.

【题目】“莲城读书月”活动结束后,对八年级(三)班45人所阅读书籍数量情况的统计结果如下表所示:
阅读数量 | 1本 | 2本 | 3本 | 3本以上 |
人数(人) | 10 | 18 | 13 | 4 |
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
A.平均数 B.中位数 C.众数 D.方差