Question

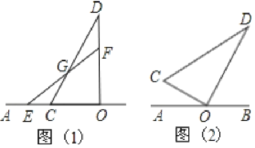
【题目】如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，连接AC.若AC=8，则四边形ABCD的面积为（　　）

A.32B.24C.40D.36

Answer 1

【答案】A

【解析】

作辅助线；证明△ABM≌△ADN，得到AM＝AN，△ABM与△ADN的面积相等；求出正方形AMCN的面积即可解决问题．

解：如图，作AM⊥BC、AN⊥CD，交CD的延长线于点N；
∵∠BAD＝∠BCD＝90°
∴四边形AMCN为矩形，∠MAN＝90°；
∵∠BAD＝90°，
∴∠BAM＝∠DAN；
在△ABM与△ADN中，

∴△ABM≌△ADN（AAS），
∴AM＝AN（设为a）；△ABM与△ADN的面积相等；
∴四边形ABCD的面积＝正方形AMCN的面积；
由勾股定理得：AC2＝AM2＋MC2，而AC＝8；
∴2a2＝64，a2＝32，
故选：A．