题目内容
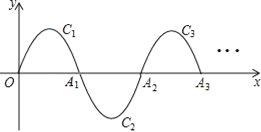
【题目】已知y1=a1(x﹣m)2+5,点(m,25)在抛物线y2=a2x2+b2x+c2上,其中m>0.
(1)若a1=﹣1,点(1,4)在抛物线y1=a1(x﹣m)2+5上,求m的值;
(2)记O为坐标原点,抛物线y2=a2x2+b2x+c2的顶点为M,若c2=0,点A(2,0)在此抛物线上,∠OMA=90°,求点M的坐标;
(3)若y1+y2=x2+16x+13,且4a2c2﹣b22=﹣8a2,求抛物线y2=a2x2+b2x+c2的解析式.
【答案】(1)m=2;(2)M(1,﹣1);(3)y2=3x2+12x+10.
【解析】试题分析:(1)把点代入求值.(2)把已知点代入可求得抛物线对称轴,由对称性可知△OAM是等腰三角形,所以可以得到M点坐标.
(3)利用待定系数法,结合已知联立方程组求解,利用代入消元技巧,可求得抛物线解析式.
试题解析:
(1)∵a1=﹣1,∴y1=﹣(x﹣m)2+5.
将(1,4)代入y1=﹣(x﹣m)2+5,得
4=﹣(1﹣m)2+5.
m=0或m=2.∵m>0,∴m=2.
(2)∵c2=0,∴抛物线y2=a2 x2+b2 x,
将(2,0)代入y2=a2 x2+b2 x,得4a2+2b2=0.即b2=﹣2a2,
∴抛物线的对称轴是x=1,
设对称轴与x轴交于点N,根据抛物线的对称性得,△OAM是等腰三角形,
∴NA=NO=1,
∵∠OMA=90°,
∴MN=OA=1,∴当a2>0时,M(1,﹣1),
当a2<0时,M(1,1),
∵25>1,∴M(1,﹣1).
(3)方法一:∵点(m,25)在抛物线y2=a2 x2+b2x+c2上,
∴a2 m 2+b2 m+c2=25①,
∵y1+y2=(a1+a2)x2+(b2﹣2a1m)x+5+a1m2+c2=x2+16x+13,
∴a1+a2=1②,b2﹣2a1m=16③,a1m2+c2=8④,
由③得,b2m=16m+2a1m2⑤,由④得,c2=8a1m2⑥,
将⑤⑥代入方程①得,a2 m 2+16m+2 m 2 a1+8﹣m 2 a1=25,
整理得,m 2+16m﹣17=0,
解得m1=1,m2=﹣17,
∵m>0,∴m=1,
将m=1代入③得,b2=16+2a1=12+2(1﹣a2)=18﹣2a2,将m=1代入④得,c2=8﹣a1=8﹣(1﹣a2)=7+a2.
∵4a2 c2﹣b22=﹣8a2,∴4a2(7+a2)﹣(18﹣2a2)2=﹣8a2,
∴a2=3,∴b2=18﹣2×3=12,c2=7+3=10,
∴抛物线y2=a2x2+b2x+c2的解析式为y=3x2+12x+10.
方法二,由题意知,当x=m时,y1=5;当x=m时,y2=25,
∴当x=m时,y1+y2=5+25=30,
∵y1+y2=x2+16 x+13,∴30=m2+16m+13.
解得m1=1,m2=﹣17.
∵m>0,∴m=1,
∵4a2 c2﹣b22=﹣8a2,∴ ![]() =
=![]() =﹣2,
=﹣2,
∴y2 顶点的纵坐标为﹣2,
设抛物线y2的解析式为y2=a2 (x﹣h)2﹣2,∴y1+y2=a1 (x﹣1)2+5+a2 (x﹣h)2﹣2.
∵y1+y2=(a1+a2)x2﹣2(a1+a2h)x+a1+a2h2+3=x2+16 x+13,∴a1+a2=1①,﹣2(a1+a2h)=16②,a1+a2h2+3=13③,将①代入②③化简得,a2h﹣a2=﹣9④,a2h2﹣a2=9⑤,联立④⑤,解得h=﹣2,a2=3,
∴抛物线的解析式为y2=3(x+2)2﹣2=3x2+12x+10.
方法三、由题意知,当x=m时,y1=5;当x=m时,y2=25,
∴当x=m时,y1+y2=5+25=30,
∵y1+y2=x2+16x+13,∴30=m2+16m+13,
∴m=1或m=﹣17,∵m>0,∴m=1,∴y1=a1 (x﹣1)+5,
∵y1+y2=x2+16x+13,∴y2=x2+16 x+13﹣y1
=x2+16x+13﹣a1 (x﹣1)2﹣5,
即y2=(1﹣a1)x2+(16+2a1)x+8﹣a1,
∵4a2c2﹣b22=﹣8a2,∴ ![]() =
=![]() =﹣2,
=﹣2,
∴y2 顶点的纵坐标为﹣2,∴ 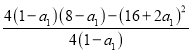 =-2,
=-2,
∴a1=﹣2,∴y2=3x2+12x+10.

 名校课堂系列答案
名校课堂系列答案