题目内容
【题目】探索规律:将连续的偶2,4,6,8,…,排成如表:
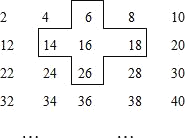
(1)请你求出十字框中的五个数的和;
(2)设中间的数为x,请你用含x的式子表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,这五个数的和能等于2018吗?如能,写出这五个数,如不能,请说明理由.
【答案】(1)80;(2)用含x的代数式表示十字框框住的5个数字之和为5x;(3)不能框住五个数,和等于2018,见解析.
【解析】
(1)将十字框中的五个数直接相加即可;
(2)分别用含x的式子表示周围4个数,然后把这5个数相加即可;
(3)设中间的数为m,根据(2)中的方法列式子求解,判断m是否为整数即可.
解:(1)十字框框出5个数的和为:6+14+16+18+26=80;
(2)根据题意得:
x上边的数字为:x﹣10,
x下边的数字为:x+10,
x左边的数字为:x﹣2,
x右边的数字为:x+2,
则十字框中的五个数字之和为:(x﹣10)+(x+10)+(x﹣2)+(x+2)+x=5x,
即用含x的代数式表示十字框框住的5个数字之和为5x;
(3)设中间的数为m,
根据题意得:5m=2018,
解得:m=403.6,
m不是整数,
即不能框住五个数,和等于2018.

练习册系列答案
相关题目