题目内容
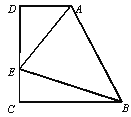
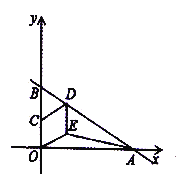
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,四边形
上一点,四边形![]() 是菱形,则
是菱形,则![]() 面积为___________.
面积为___________.
【答案】![]()
【解析】
延长DE交OA于F,如图,先利用一次函数解析式确定B(0,4),A(6![]() ,0),利用三角函数得到∠OBA=60°,接着根据菱形的性质判定△BCD为等边三角形,则∠BCD=∠COE=60°,所以∠EOF=30°,则
,0),利用三角函数得到∠OBA=60°,接着根据菱形的性质判定△BCD为等边三角形,则∠BCD=∠COE=60°,所以∠EOF=30°,则![]() ,然后根据三角形面积公式计算.
,然后根据三角形面积公式计算.
解:延长DE交OA于F,如图,
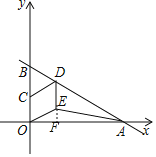
当x=0时,![]() ,则B(0,4),
,则B(0,4),
当y=0时,![]() ,解得x=6
,解得x=6![]() ,则A(6
,则A(6![]() ,0)
,0)
在Rt△AOB中,![]()
∴∠OBA=60°,
∵C是OB的中点,
∴OC=CB=3,
∵四边形OEDC是菱形,
∴CD=BC=DE=CE=3,CD∥OE,
∴△BCD为等边三角形,
∴∠BCD=60°,
∴∠COE=60°,
∴∠EOF=30°,
![]()
△OAE的面积![]()
故答案为: ![]()

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
【题目】为缓解油价上涨给出租车行业带来的成本压力,某市拟调整出租车运价,调整方案见下列表格及图象(其中![]() 为常数)
为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过 | 起步价7元 | 起步价 |
超过 | 每公里2元 | 每公里 |
超出 | 每公里 | |
设行驶路程为![]() ,调价前的运价
,调价前的运价![]() (元),调价后运价
(元),调价后运价![]() (元),如图,折线
(元),如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系式,线段
之间的函数关系式,线段![]() 表示当
表示当![]() 时,
时,![]() 与
与![]() 的函数关系式,根据图表信息,完成下列各题:
的函数关系式,根据图表信息,完成下列各题:
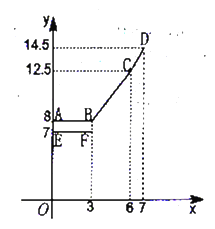
①填空:![]() ,
,![]() ,
,![]() ;
;
②当![]() 时,求
时,求![]() 与
与![]() 的关系,补充图中该函数的图像;
的关系,补充图中该函数的图像;
③函数![]() 与
与![]() 的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.